Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 1 | H2 Maths
4 Answers Below
Anyone can contribute an answer, even non-tutors.

Confuse on how to determine part ii
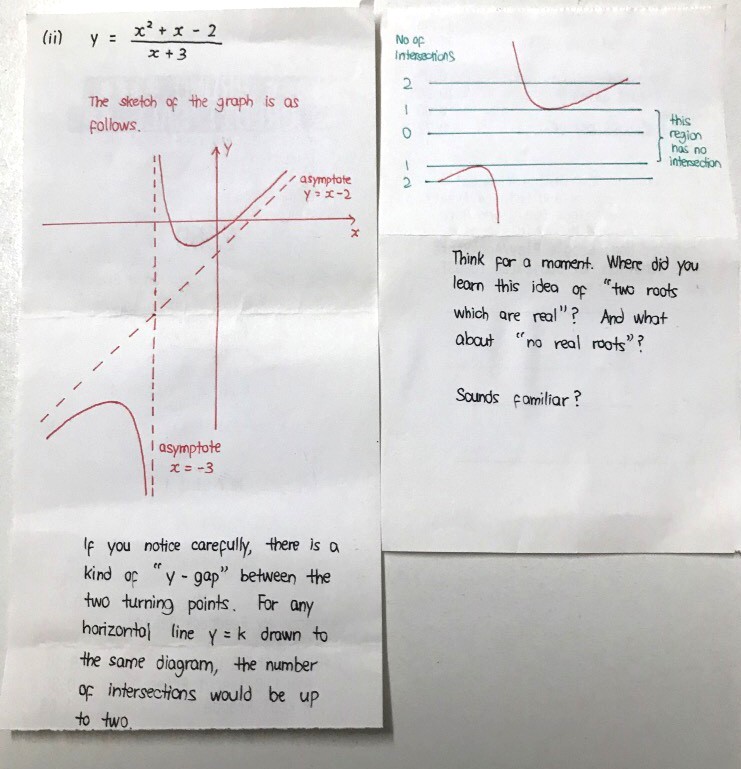
Horizontal lines do not always cut the graph because the graph does not appear for some values of y. It's like a smiley face graph ending at say y = 4 and a sad face graph ending at say y = -4. Then there is no "graph" between y = -4 and y = 4.
For some values y = k, the graph will not exist. However, for those which the graph does exist, it will only cut the curve at most twice, which is largely similar to how you would solve discriminant questions.
Let k = that fraction for curve C.
Then k (x + r) = x² + px - q.
We will transform this into the form ax² + bx + c = 0, where discriminant < 0 for the "missing" range for the original curve.
Will do this later if no one responds by tonight.
See 4 Answers
x² + px - q = 0 (because y can only equal zero when the numerator is zero but the denominator is non-zero)
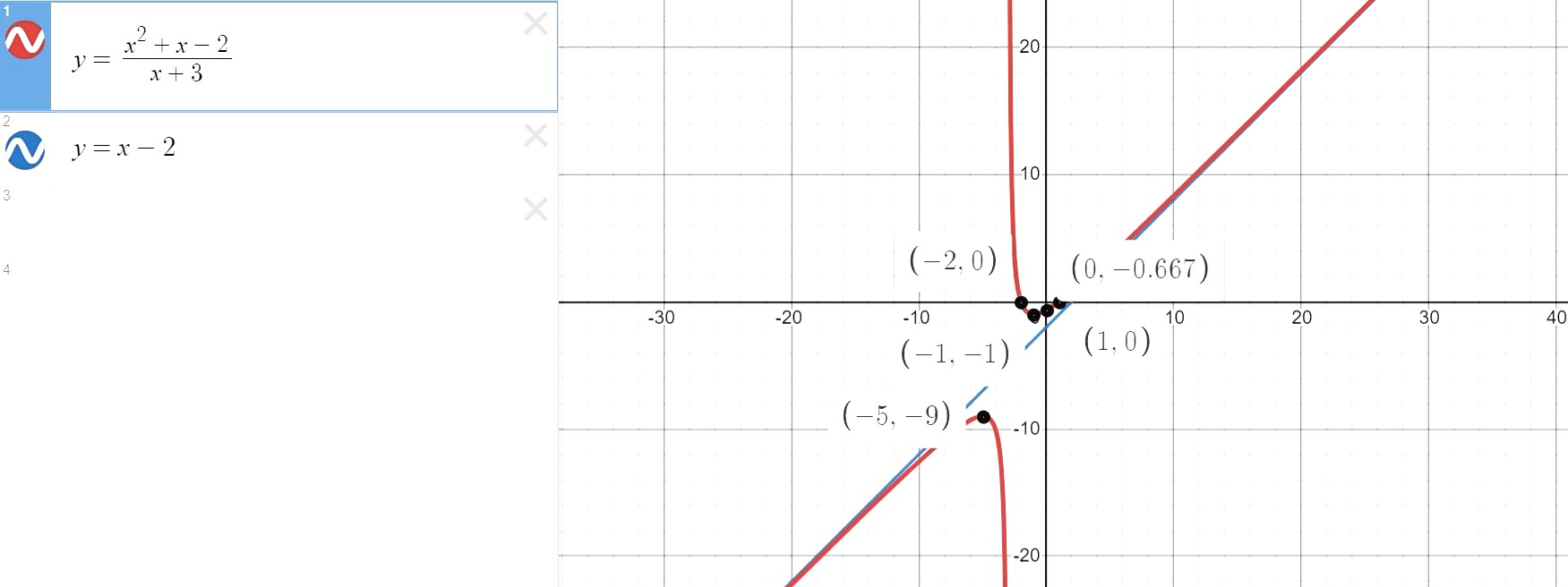
From the roots at x = -2 and x = 1,
(x + 2) (x - 1) = 0
x² - x + 2x - 2 = 0
x² + x - 2 = 0
Comparing,
p = 1, q = 2
(note that q = 2 and not q = -2)
3x⁴ + 3x³ - 6x² - x - 3 = 0
3x⁴ + 3x³ - 6x² = x + 3
3x² (x² + x - 2) = x + 3
Cross-dividing,
(x² + x - 2) / (x + 3) = 1 / (3x²)
The left-hand side of this equation is your original curve C, while the right-hand side of this equation is the new curve which you will have to draw, i.e.
y = 1 / (3x²)
One is close to x = -2, while the other is close to x = 1.25.
There are no intersections with the sad face portion of curve C.
So total, there are two intersections of the two curves, meaning to say that there are exactly two real roots to the equation 3x⁴ + 3x³ - 6x² - x - 3 = 0.
[In reality, there are two other roots, but they are complex/imaginary/non-real roots]