Eric Nicholas K's answer to 111's Junior College 1 H2 Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
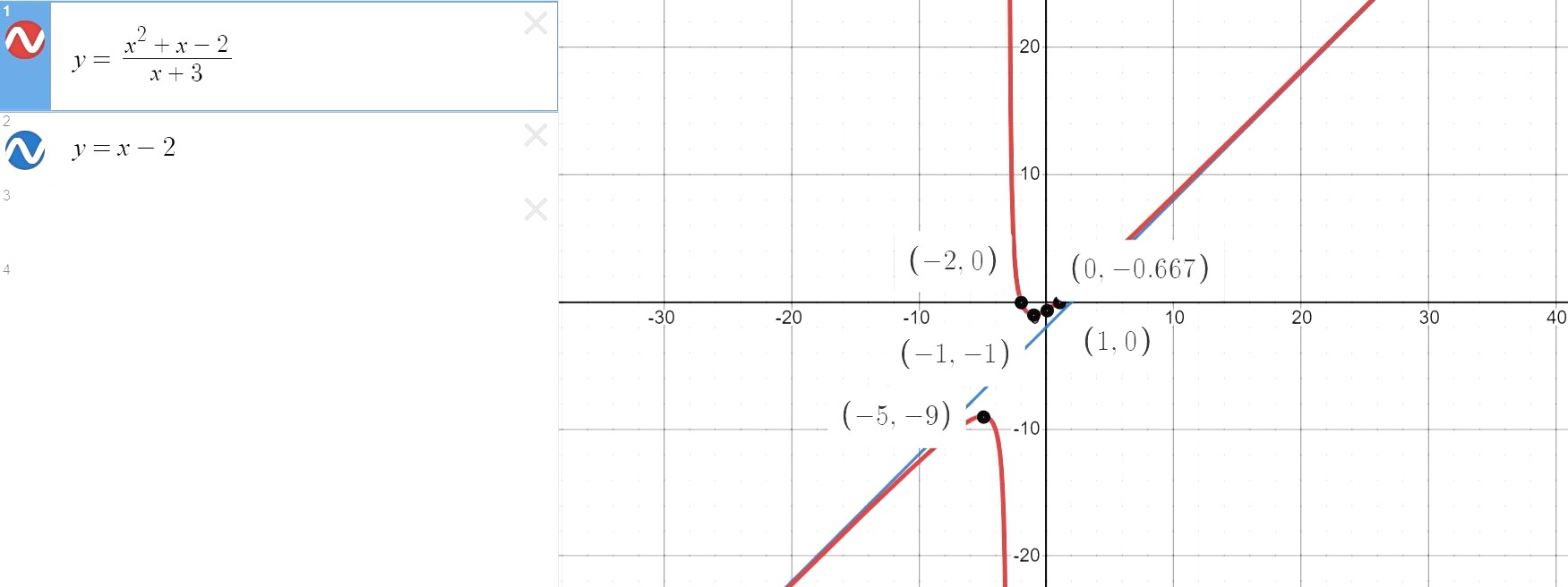
You can tag the points down to the diagram for part (iii) which I have drawn in my "prelude" section earlier.
Date Posted:
3 years ago
For part iv, do this:
3x⁴ + 3x³ - 6x² - x - 3 = 0
3x⁴ + 3x³ - 6x² = x + 3
3x² (x² + x - 2) = x + 3
Cross-dividing,
(x² + x - 2) / (x + 3) = 1 / (3x²)
The left-hand side of this equation is your original curve C, while the right-hand side of this equation is the new curve which you will have to draw, i.e.
y = 1 / (3x²)
3x⁴ + 3x³ - 6x² - x - 3 = 0
3x⁴ + 3x³ - 6x² = x + 3
3x² (x² + x - 2) = x + 3
Cross-dividing,
(x² + x - 2) / (x + 3) = 1 / (3x²)
The left-hand side of this equation is your original curve C, while the right-hand side of this equation is the new curve which you will have to draw, i.e.
y = 1 / (3x²)
There will only be two intersecting points with the smiley face portion of curve C.
One is close to x = -2, while the other is close to x = 1.25.
There are no intersections with the sad face portion of curve C.
So total, there are two intersections of the two curves, meaning to say that there are exactly two real roots to the equation 3x⁴ + 3x³ - 6x² - x - 3 = 0.
[In reality, there are two other roots, but they are complex/imaginary/non-real roots]
One is close to x = -2, while the other is close to x = 1.25.
There are no intersections with the sad face portion of curve C.
So total, there are two intersections of the two curves, meaning to say that there are exactly two real roots to the equation 3x⁴ + 3x³ - 6x² - x - 3 = 0.
[In reality, there are two other roots, but they are complex/imaginary/non-real roots]