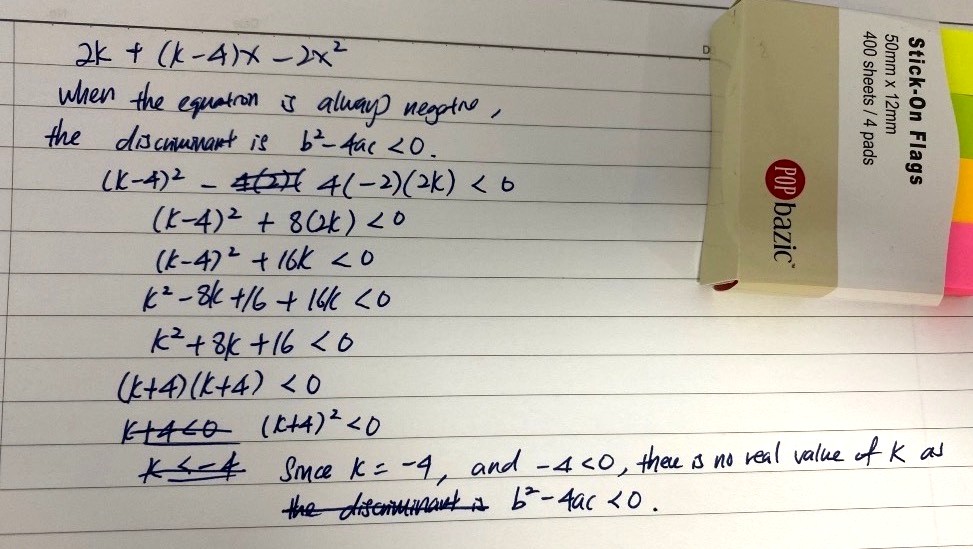Nono. You've mixed up b² - 4ac < 0 and ' expression is always negative'

Or rather, you have to show the logical link as to why discriminant < 0


When 2k + (k - 4)x - 2x² is always negative,
the curve y = 2k + (k - 4)x - 2x² does not intersect the x-axis at all.

It is always below the x-axis, where y = 0

Therefore , there are no real roots to the equation 2k + (k - 4)x - 2x² = 0 . So, discriminant < 0


From that part of your working, to ' (k + 4)² < 0 ', it is correct.


But it is not correct to say that k = -4 , because k ≠ -4


You should add the following :

Since (k + 4)² ≥ 0 for all real values of k, when (k + 4)² < 0, there are no real values of k such that 2k + (k - 4)x - 2x² is always negative.

(Reasoning : the square of any real number is always 0 or positive)

Here we try to "show" something.

So, we cannot put the "< 0" statement in every line, because then we would already be assuming it to be true in the process of showing it.

We must not write the "< 0" portion until the very end.

Better is

Discriminant of roots
= (k - 4)² - 4 (2k) (-2)
= k² - 8k + 16 + 16k
= k² + 8k + 16
= (k + 4)²
≥ 0 for all real values of k

[This is because a perfect square does not contain any negative output values naturally]

Since the discriminant of roots is more than or equal to zero, the curve is bound to intersect the x-axis at least once when drawn on a graph.

This means that the graph will have an output value of 0 for some values of x (for every value of k considered), and therefore, we cannot have real values of k which make the graph "always negative" (i.e. entirely below the x-axis, since this implies no intersection with the x-axis).

@Eric :

You've misunderstood the question.

The question is trying to ask the student to show there are no real values of k for which 2k + (k - 4)x - 2x² is always negative.

It is not trying to ask the student to show that 2k + (k - 4)x - 2x² is always negative. If that were the case, writing 2k + (k - 4)x - 2x² < 0 would be assuming the premise is true when trying to prove it.


So the approach should be :

'For 2k + (k - 4)x - 2x² is always negative (< 0) , I have to show that I cannot have any real values of k'

So we have to start from the premise that 2k + (k - 4)x - 2x² < 0.

What we cannot assume is that the values of k ARE already non-real.

For Eric’s working, how did you get (k+4)^2 ≥ 0 for all real value of k? I thought (k+4)^2 < 0?

This is the part that is in the answer key but I don’t understand about

If I follow J’s explanation, wouldn’t (k+4)^2 < 0?

Your approach can be summarised by the following :

For 2k + (k - 4)x - 2x² = 0

Discriminant = (k + 4)²

Then you made the proposition that if k is real, (k + 4)² ≥ 0 for all real k

This is taking k to be real already. i.e assuming.

Next, since the discriminant ≥ 0 for all real k, there is at least one point of intersection of the curve y = 2k + (k - 4)x - 2x² with y = 0

Or in other words, 2k + (k - 4)x - 2x² = 0 for some value of x.

So 2k + (k - 4)x - 2x² cannot be always negative if k is real. So there are no real values of k where it is always negative.

This is actually similar to proof by contradiction, where you assume something to be true first (i.e k is real for an always negative 2k + (k - 4)x - 2x²) and then show that a contradiction results from that (2k - (k-4)x - 2x² is not always negative and is 0 for some x)

There is a difference in the approach used by me and his approach.

QN, basically my idea here is to show that our discriminant cannot have a negative value, against what is expected of an "always negative" curve.

The fact that (k + 4)² is always positive is testament to the fact that we cannot extract a negative value of (k + 4)², which is why we cannot have situations where the curve is always negative.

This is why we can never find a real value of k which makes the discriminant (k + 4)² negative.

I finally understand. Thank you both for the detailed explanation.

By the way, it is not correct to say perfect square. k is not defined to be an integer.

Not quite accurate to to say that the discriminant cannot have a negative value.

It cannot have a negative value IF you take k to be real.

In my approach, I have already shown that (k + 4)² < 0 for an always negative 2k + (k - 4)x - 2x², which in turn means that k + 4 (and in turn k) is always non-real for this case.

So there are no real values of k for this case.