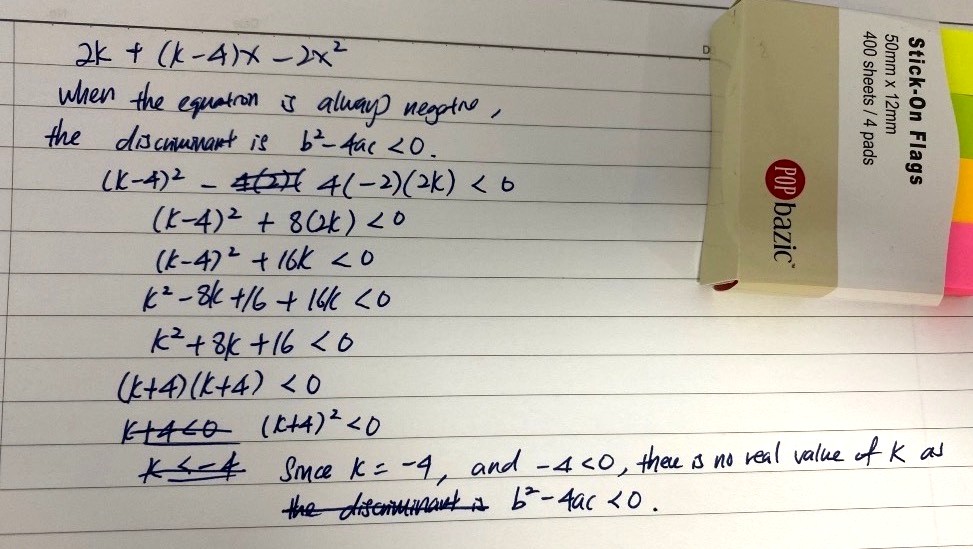Nono. You've mixed up b² - 4ac < 0 and ' expression is always negative'

Or rather, you have to show the logical link as to why discriminant < 0


When 2k + (k - 4)x - 2x² is always negative,
the curve y = 2k + (k - 4)x - 2x² does not intersect the x-axis at all.

It is always below the x-axis, where y = 0

Therefore , there are no real roots to the equation 2k + (k - 4)x - 2x² = 0 . So, discriminant < 0


From that part of your working, to ' (k + 4)² < 0 ', it is correct.


But it is not correct to say that k = -4 , because k ≠ -4


You should add the following :

Since (k + 4)² ≥ 0 for all real values of k, when (k + 4)² < 0, there are no real values of k such that 2k + (k - 4)x - 2x² is always negative.

(Reasoning : the square of any real number is always 0 or positive)

Here we try to "show" something.

So, we cannot put the "< 0" statement in every line, because then we would already be assuming it to be true in the process of showing it.

We must not write the "< 0" portion until the very end.

Better is

Discriminant of roots
= (k - 4)² - 4 (2k) (-2)
= k² - 8k + 16 + 16k
= k² + 8k + 16
= (k + 4)²
≥ 0 for all real values of k

[This is because a perfect square does not contain any negative output values naturally]

Since the discriminant of roots is more than or equal to zero, the curve is bound to intersect the x-axis at least once when drawn on a graph.

This means that the graph will have an output value of 0 for some values of x (for every value of k considered), and therefore, we cannot have real values of k which make the graph "always negative" (i.e. entirely below the x-axis, since this implies no intersection with the x-axis).

@Eric :

You've misunderstood the question.

The question is trying to ask the student to show there are no real values of k for which 2k + (k - 4)x - 2x² is always negative.

It is not trying to ask the student to show that 2k + (k - 4)x - 2x² is always negative. If that were the case, writing 2k + (k - 4)x - 2x² < 0 would be assuming the premise is true when trying to prove it.


So the approach should be :

'For 2k + (k - 4)x - 2x² is always negative (< 0) , I have to show that I cannot have any real values of k'

So we have to start from the premise that 2k + (k - 4)x - 2x² < 0.

What we cannot assume is that the values of k ARE already non-real.

For Eric’s working, how did you get (k+4)^2 ≥ 0 for all real value of k? I thought (k+4)^2 < 0?

This is the part that is in the answer key but I don’t understand about

If I follow J’s explanation, wouldn’t (k+4)^2 < 0?

Your approach can be summarised by the following :

For 2k + (k - 4)x - 2x² = 0

Discriminant = (k + 4)²

Then you made the proposition that if k is real, (k + 4)² ≥ 0 for all real k

This is taking k to be real already. i.e assuming.

Next, since the discriminant ≥ 0 for all real k, there is at least one point of intersection of the curve y = 2k + (k - 4)x - 2x² with y = 0

Or in other words, 2k + (k - 4)x - 2x² = 0 for some value of x.

So 2k + (k - 4)x - 2x² cannot be always negative if k is real. So there are no real values of k where it is always negative.

This is actually similar to proof by contradiction, where you assume something to be true first (i.e k is real for an always negative 2k + (k - 4)x - 2x²) and then show that a contradiction results from that (2k - (k-4)x - 2x² is not always negative and is 0 for some x)

There is a difference in the approach used by me and his approach.

QN, basically my idea here is to show that our discriminant cannot have a negative value, against what is expected of an "always negative" curve.

The fact that (k + 4)² is always positive is testament to the fact that we cannot extract a negative value of (k + 4)², which is why we cannot have situations where the curve is always negative.

This is why we can never find a real value of k which makes the discriminant (k + 4)² negative.

I finally understand. Thank you both for the detailed explanation.

By the way, it is not correct to say perfect square. k is not defined to be an integer.

Not quite accurate to to say that the discriminant cannot have a negative value.

It cannot have a negative value IF you take k to be real.

In my approach, I have already shown that (k + 4)² < 0 for an always negative 2k + (k - 4)x - 2x², which in turn means that k + 4 (and in turn k) is always non-real for this case.

So there are no real values of k for this case.

It was supposed to lead to b^2-4ac < 0. But how did (k+4)^2 ended up ≥ 0

We would actually like our discriminant

(k + 4)²

to be negative for the purposes of this question.

However, this can never happen, as (k + 4)² is naturally a non-negative expression for all real values of k.

The answer scheme uses such an approach :

① For an always negative 2k + (k - 4)x - 2x²,
the discriminant < 0 (since it does not intersect the x-axis where y = 0 , which means there are no real roots of x)

② Now the discriminant = (k + 4)² .

If k is real, then k + 4 is also real.

So for all real values of k, (k + 4)² ≥ 0 (since the square of any real value is either 0 or positive) . So the discriminant will have to be ≥ 0


③ But in ① , we have already made the conclusion that the discriminant < 0 for an always negative 2k + (k - 4)x - 2x²

④ We can now conclude that there are no real values of k for which 2k + (k - 4)x - 2x² is always negative, since for all real values of k the discriminant is always positive or 0 (edited)

I remember one of my students asking me about this "discrepancy" because the logical sense seems weird. I had to do the explaining for my student because he was confused with the signages.

Do take note QN, that this answer scheme is published by the series publisher and not by Cambridge. So it really depends on what the markers there accept.

I see where the answer key is coming from. Thank you for the detailed explanation!

My approach was :

① For an always negative 2k + (k - 4)x - 2x²,
there is no intersection of the curve y = 2k + (k - 4)x - 2x² with the x-axis (where y = 0)

② This means that there are no real roots so discriminant < 0

③ Discriminant is found to be (k + 4)².

So for discriminant < 0, (k + 4)² < 0

④ Since (k + 4)² < 0, k is non-real.

Because for all real k, (k + 4)² ≥ 0.
So k cannot be real.


⑤ Therefore there are no real values of k for which 2k + (k - 4)x - 2x² is always negative.