glittr's answer to glittr's Secondary 4 A Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
updated qn
Date Posted:
5 years ago
It’s not that straightforward.
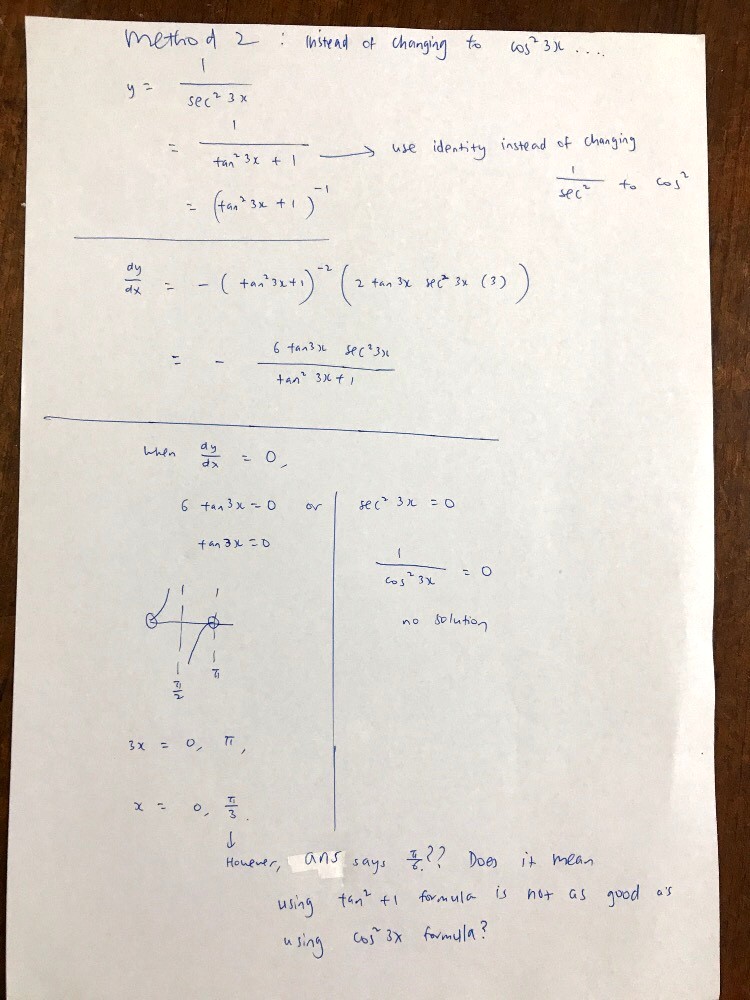
Strictly speaking, it’s not just the sec^2 3x which is invalid when x = pi/6. The tan^2 3x in the denominator is also technically undefined when x = pi/6.
The fact that the point pi/6 does exist in the original graph means we need to somehow modify our expression for dy/dx (by the way, your denominator should be the whole thing squared).
I will have a look at this again when I am more free.
Strictly speaking, it’s not just the sec^2 3x which is invalid when x = pi/6. The tan^2 3x in the denominator is also technically undefined when x = pi/6.
The fact that the point pi/6 does exist in the original graph means we need to somehow modify our expression for dy/dx (by the way, your denominator should be the whole thing squared).
I will have a look at this again when I am more free.
I just observed. Your expression for dy/dx can further be simplified. We return our denominator to (sec^2 3x)^2, and then simplify to -6 Tan 3x divided by sec^2 3x, which is -6 tan 3x cos^2 3x.
This is where you can set dy/dx to 0.
Rather, this second approach is actually quite invalid because your introduction of the secant renders the pi/6 solution inadmissible (since secant of 3 pi/6 is undefined).
This is where you can set dy/dx to 0.
Rather, this second approach is actually quite invalid because your introduction of the secant renders the pi/6 solution inadmissible (since secant of 3 pi/6 is undefined).
In short, this approach fails because of the unnecessary introduction of the secant function which causes pi/6 to be invalid.
is using secant considered an “unlucky “ method ? like we wouldn’t know in the beginning if it could work or fail
It’s not just secant which falls prey to this approach. Any approach which causes a denominator to be formed usually creates this issue.
Take for example the simplest case.
Solve x - 3 = 0.
One can easily say that x = 3.
But why not we do this?
x - 3 = (x - 3)^2 / (x - 3)
They are the same, but the unnecessary introduction of the denominator causes the same solution x = 3 to be rejected, in view that denominators cannot be equated to zero.
For the same idea, secant fails miserably here.
Take for example the simplest case.
Solve x - 3 = 0.
One can easily say that x = 3.
But why not we do this?
x - 3 = (x - 3)^2 / (x - 3)
They are the same, but the unnecessary introduction of the denominator causes the same solution x = 3 to be rejected, in view that denominators cannot be equated to zero.
For the same idea, secant fails miserably here.
Logarithmic functions also have this problem. This is the reason why the solutions to
ln x^2 = 0
and
2 ln x = 0
are different, even though both equations are immediately interchangeable by the logarithmic rules. The solutions are x = -1 and x = 1, but all because ln (-1) is undefined, we reject the solution x = -1 for the 2 ln x = 0 case.
So if a question is posed as ln x^2 = 0, taking the approach 2 ln x = 0 instead of converting to the index form x^2 = 1 causes us to lose the negative solution which would have otherwise been valid.
ln x^2 = 0
and
2 ln x = 0
are different, even though both equations are immediately interchangeable by the logarithmic rules. The solutions are x = -1 and x = 1, but all because ln (-1) is undefined, we reject the solution x = -1 for the 2 ln x = 0 case.
So if a question is posed as ln x^2 = 0, taking the approach 2 ln x = 0 instead of converting to the index form x^2 = 1 causes us to lose the negative solution which would have otherwise been valid.
One more.
Solve 2x = 0.
Method 1: Correct
Dividing both sides by 2, x = 0.
Method 2: Flawed
2 / (1/x) = 0
1/x = 2/0
= infinity
x = 1/infinity
= 0
The secant idea closely follows this example.
Solve 2x = 0.
Method 1: Correct
Dividing both sides by 2, x = 0.
Method 2: Flawed
2 / (1/x) = 0
1/x = 2/0
= infinity
x = 1/infinity
= 0
The secant idea closely follows this example.
wow thanks for the detailed explanation . i never knew that introducing denominators are considered dangerous