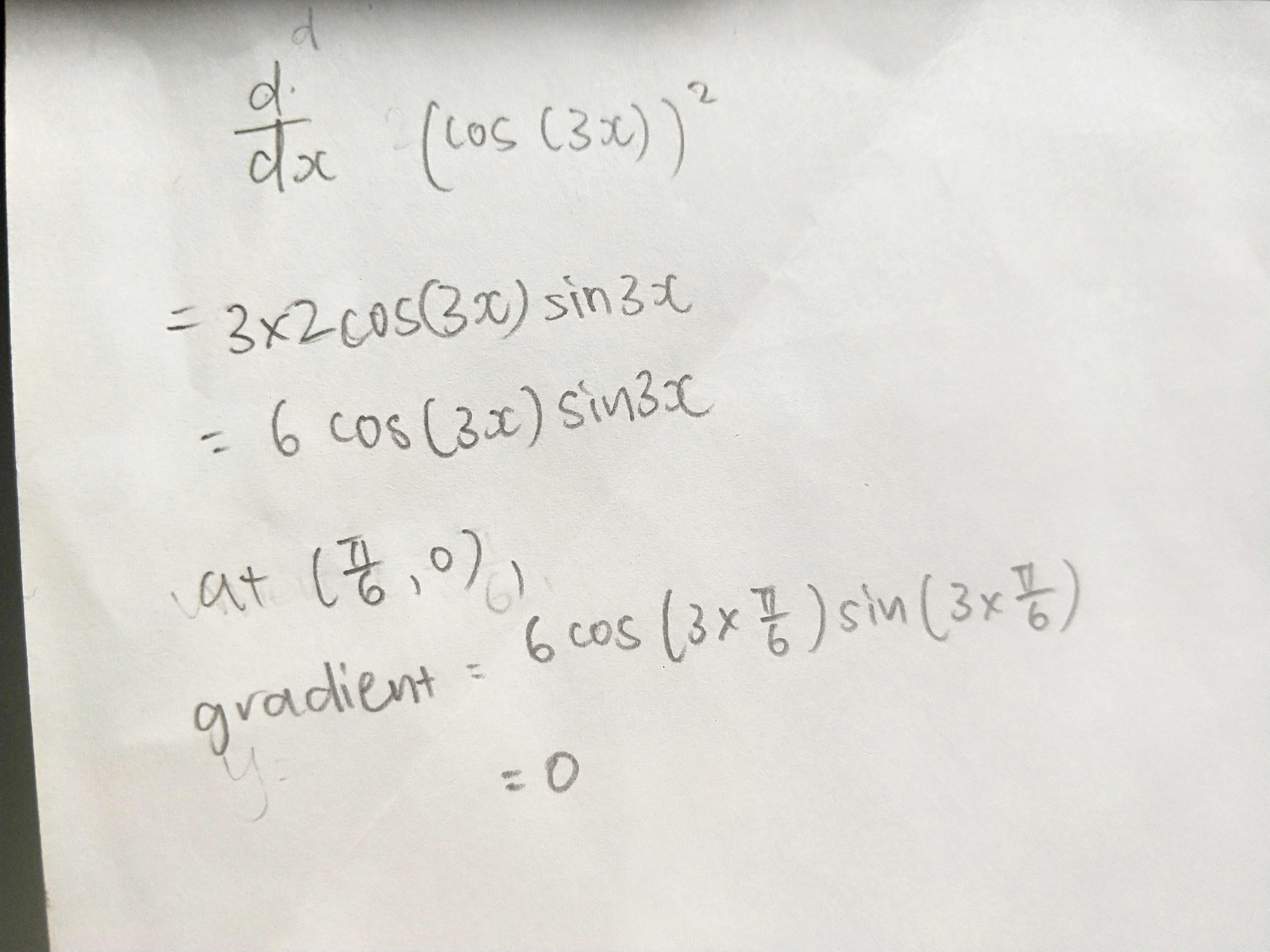Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | A Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

hi pls help with qn in the picture.
i tried but i get “undefined” answer .
In your online calculator, you must put them as such. Do not put the function y = cos (3x)^2, because the online calculator recognises this as cos (9x^2) which is entirely different. However, y = (cos 3x)^2 is perfectly ok.
y = [cos (3x)]^2
dy/dx
= 2 [cos (3x)]^1 * d/dx [cos (3x)] by the chain rule
= 2 cos (3x) * [- sin (3x)] * d/dx (3x) by a second chain rule
= -2 cos (3x) sin (3x) * 3
= -6 sin (3x) cos (3x)
When x = pi/2 (which is 90 degrees)
dy/dx
= -6 sin (3pi/2) cod (3pi/2)
= -6 (-1) (0)
(because sin 270 = -1 and cos 270 = 0, this can be seen by drawing the most basic sine and cosine graphs)
= 0
denoting that the gradient of the curve at (pi/2, 0) is 0.
You can think of y = [cos (3x)]^2 as a perfect square y = Z^2 where Z = cos (3x). As we all know, the minimum possible value of a perfect square is 0, so the curve cannot possibly have a negative y-value.
Hence, the graph must turn at the lowest value of 0, and at this turning point the gradient is zero.
The graph has a maximum value of 1, because the original un-squared function cos (3x) has a defined interval of -1 <= value <= 1 and squaring this interval gets us 0 <= value <= -1
See 2 Answers
Having said that, the missing negative sign should not affect the solution.
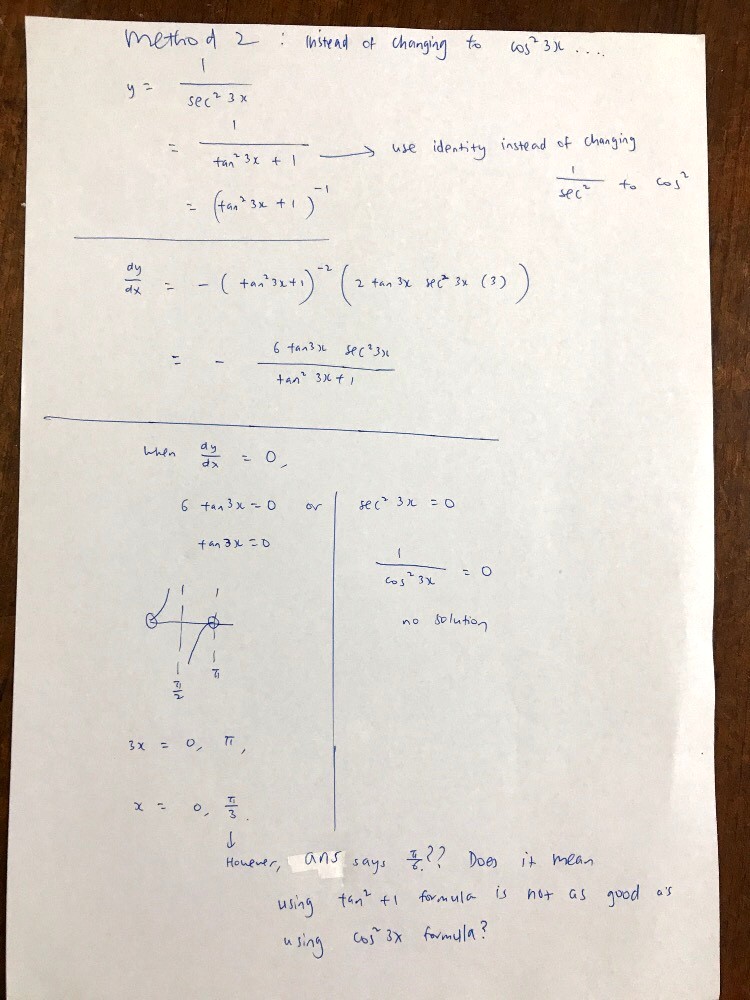
Strictly speaking, it’s not just the sec^2 3x which is invalid when x = pi/6. The tan^2 3x in the denominator is also technically undefined when x = pi/6.
The fact that the point pi/6 does exist in the original graph means we need to somehow modify our expression for dy/dx (by the way, your denominator should be the whole thing squared).
I will have a look at this again when I am more free.
This is where you can set dy/dx to 0.
Rather, this second approach is actually quite invalid because your introduction of the secant renders the pi/6 solution inadmissible (since secant of 3 pi/6 is undefined).
Take for example the simplest case.
Solve x - 3 = 0.
One can easily say that x = 3.
But why not we do this?
x - 3 = (x - 3)^2 / (x - 3)
They are the same, but the unnecessary introduction of the denominator causes the same solution x = 3 to be rejected, in view that denominators cannot be equated to zero.
For the same idea, secant fails miserably here.
ln x^2 = 0
and
2 ln x = 0
are different, even though both equations are immediately interchangeable by the logarithmic rules. The solutions are x = -1 and x = 1, but all because ln (-1) is undefined, we reject the solution x = -1 for the 2 ln x = 0 case.
So if a question is posed as ln x^2 = 0, taking the approach 2 ln x = 0 instead of converting to the index form x^2 = 1 causes us to lose the negative solution which would have otherwise been valid.
Solve 2x = 0.
Method 1: Correct
Dividing both sides by 2, x = 0.
Method 2: Flawed
2 / (1/x) = 0
1/x = 2/0
= infinity
x = 1/infinity
= 0
The secant idea closely follows this example.