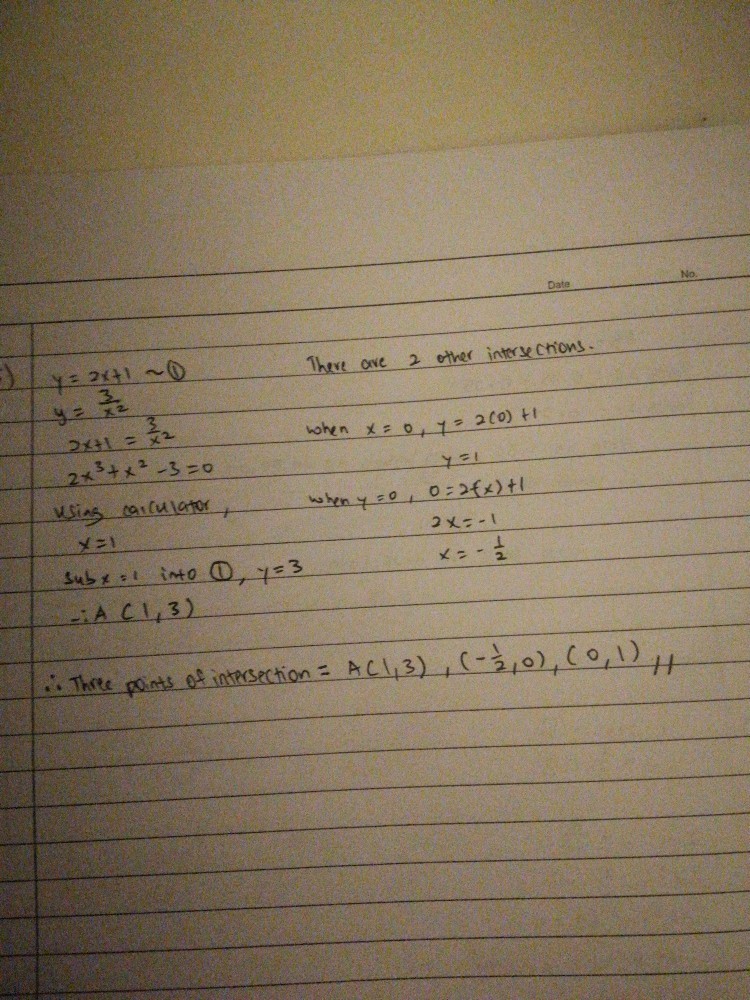Iyan's answer to uwu's Secondary 3 A Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
For qn (5). There are three intersections. For the first two, you need only sub into x=0 and y=0 as the line passes through both the x-axis and y-axis. The harder one to find is the intersection between the tangent and the curve. All you need to do is to do simultaneous equation. At the cubic part, I'm pretty sure using the calculator is fine. You can solve 2x^3 + x^2 - 3 =0 using mode/3/then 4. Not sure if it is the same for you as my calc is from a fewer versions back. You should get x=1 and two other that are nullified which is right since there is only one intersection between them. Sub in x=1 to either eqn and you'll get y=3. So A is (1,3)
Date Posted:
5 years ago
Finding the intersection points between y=2x+1 and the axes is not required as question asks for coordinates of A , i.e points of intersection between the two functions.
As for the calculator part, it can be used to find the root fast/check if root found by inspection is correct, but working must still be shown.
i.e sub x = 1 and find that f(1) = 0 so (x -1) is a factor by the Factor Theorem. Not doing so and the subsequent factorisation will result in loss of marks.
Since the question asks for any other points of intersection , it has to be shown that there are no other real roots other than x = 1 by showing discriminant < 0 for 2x² + 3 = 0. Then it can be concluded that there are no other intersections.
As for the calculator part, it can be used to find the root fast/check if root found by inspection is correct, but working must still be shown.
i.e sub x = 1 and find that f(1) = 0 so (x -1) is a factor by the Factor Theorem. Not doing so and the subsequent factorisation will result in loss of marks.
Since the question asks for any other points of intersection , it has to be shown that there are no other real roots other than x = 1 by showing discriminant < 0 for 2x² + 3 = 0. Then it can be concluded that there are no other intersections.