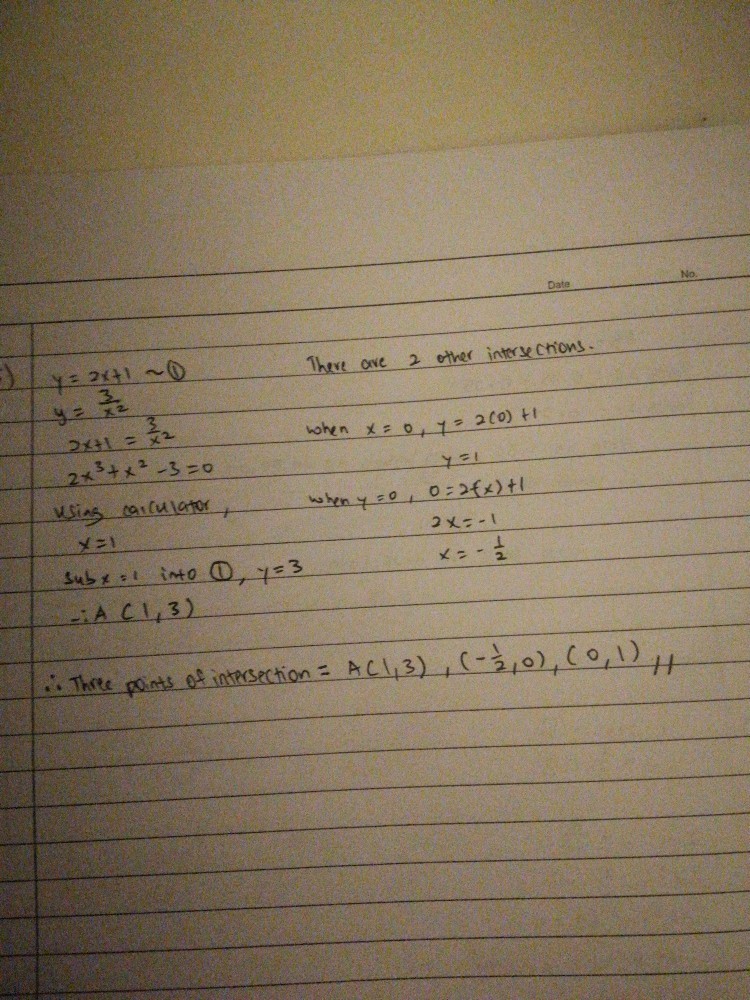Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Hi, does anyone know how to do question 5 and 6? I know that in q5 there aren’t any intersections, but I tried to solve it and I got a cubic equation and I just got stuck trying to find coordinates A. Thank you in advance
From there we just solve the polynomial as though it were a polynomial question from the start.
2x³ + x² = 3
2x³ + x² - 3 = 0
sub values of x to try.
sub x = 1,
2(1)³ + (1)² - 3 = 2 + 1 - 3 = 0
By the factor theorem, (x - 1) is a factor.
(x - 1)(2x² + 3x + 3) = 0
You can either use long division or do it mentally
so x = 1 or 2x² + 3x + 3 = 0
For 2x² + 3x + 3 = 0,
Discriminant(b² - 4ac)
= 3² - 4(2)(3)
= 9 - 24
= -15 < 0
Since discriminant < 0, there are no real roots of x for 2x² + 3 = 0
So x = 1 is the only real x-coordinate of intersection.
Or
2x² + 3x + 3 = 0
Using quadratic formula,
x = ( -3 ± √(3² - 4(2)(3) ) / (2(2) )
x = (-3 ± √-15 )/4
There are no real roots of x here as √-15 gives a non-real/imaginary number.
Therefore,
y = 2(1) + 1 = 3
Or
y = 3/1² = 3
Rewrite the equation in the form
(x - a)² + (y - b)² = r² first.
Then (a,b) is your centre.
Any chord of the circle can be perpendicularly bisected by a certain radius of the circle.
Since the perpendicular bisector passes through the centre, use the points (a,b) and M(2,3) to find its gradient as they lie on it.
Then since it's perpendicular to the chord,
Gradient of chord = -1/gradient of perpendicular bisector of chord
So for y = mx + c, you already know m now.
Since M(2,3) lies on the chord as well ,
Sub the coordinates in to find c. Then you have your answer.
The x and y axis are asymptotes of the curve y = 3/x² (x tends to 0 but doesn't reach 0 as y tends to infinity, vice versa) so the curve never intersects them.
And there is no part of the curve on and below the x-axis (i.e no values of y ≤ 0).
So the curve doesn't intersect the portion of y = 2x + 1 for those regions.
As for above the x-axis, the intersection is only at A for the region between the curve.
From point A, as x tends to infinity, y is strictly increasing and tends to infinity for y = 2x + 1.
But for y = 3/x², as x tends to infinity, y is strictly decreasing and tends to 0.
So the values of y are heading in diametrically opposite directions as thus there are no more intersections.
See 1 Answer
As for the calculator part, it can be used to find the root fast/check if root found by inspection is correct, but working must still be shown.
i.e sub x = 1 and find that f(1) = 0 so (x -1) is a factor by the Factor Theorem. Not doing so and the subsequent factorisation will result in loss of marks.
Since the question asks for any other points of intersection , it has to be shown that there are no other real roots other than x = 1 by showing discriminant < 0 for 2x² + 3 = 0. Then it can be concluded that there are no other intersections.