According to question, QR = TR. and since PQRS is a square, QR = RS too. Therefore, QR = TR = RS, which makes the angle RTS = angle RST.

The second part of your working is incorrect. The two triangles are isosceles, but they are not neither similar nor congruent.

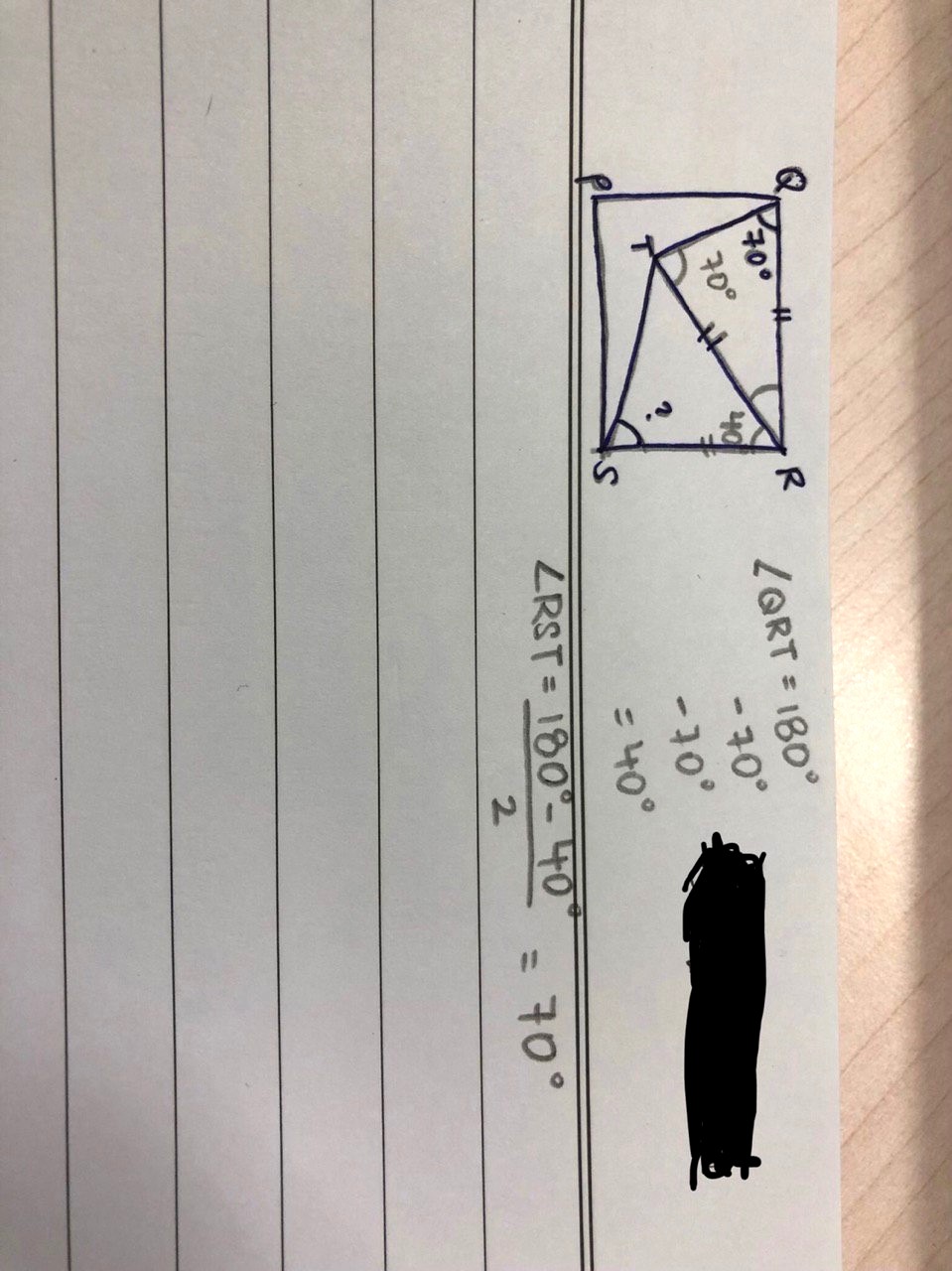
Angle TRS cannot be 40° as the sum of angle TRS and angle QRT (which gives QRS) would then be 80°, but QRS is actually a right angle (90°), which is a contradiction.


angle TRS = angle QRS - angle QRT
= 90° - 40°
= 50°

Angle RST = (180° - 50°)/2 = 65°

Apologies, I labeled 40* at the wrong location causing the mistake. It should be 90* - 40* = 50* then 180* - 50* = 130* divide by 2 = 65*.

Thank you.