Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
primary 6 | Maths
| Geometry
One Answer Below
Anyone can contribute an answer, even non-tutors.

Please help, thank you.
△QRT is isosceles.
QR also = SR (both are sides of a square)
So TR = SR
△ SRT is also isosceles
Use the properties of an isosceles triangle to solve
See 1 Answer



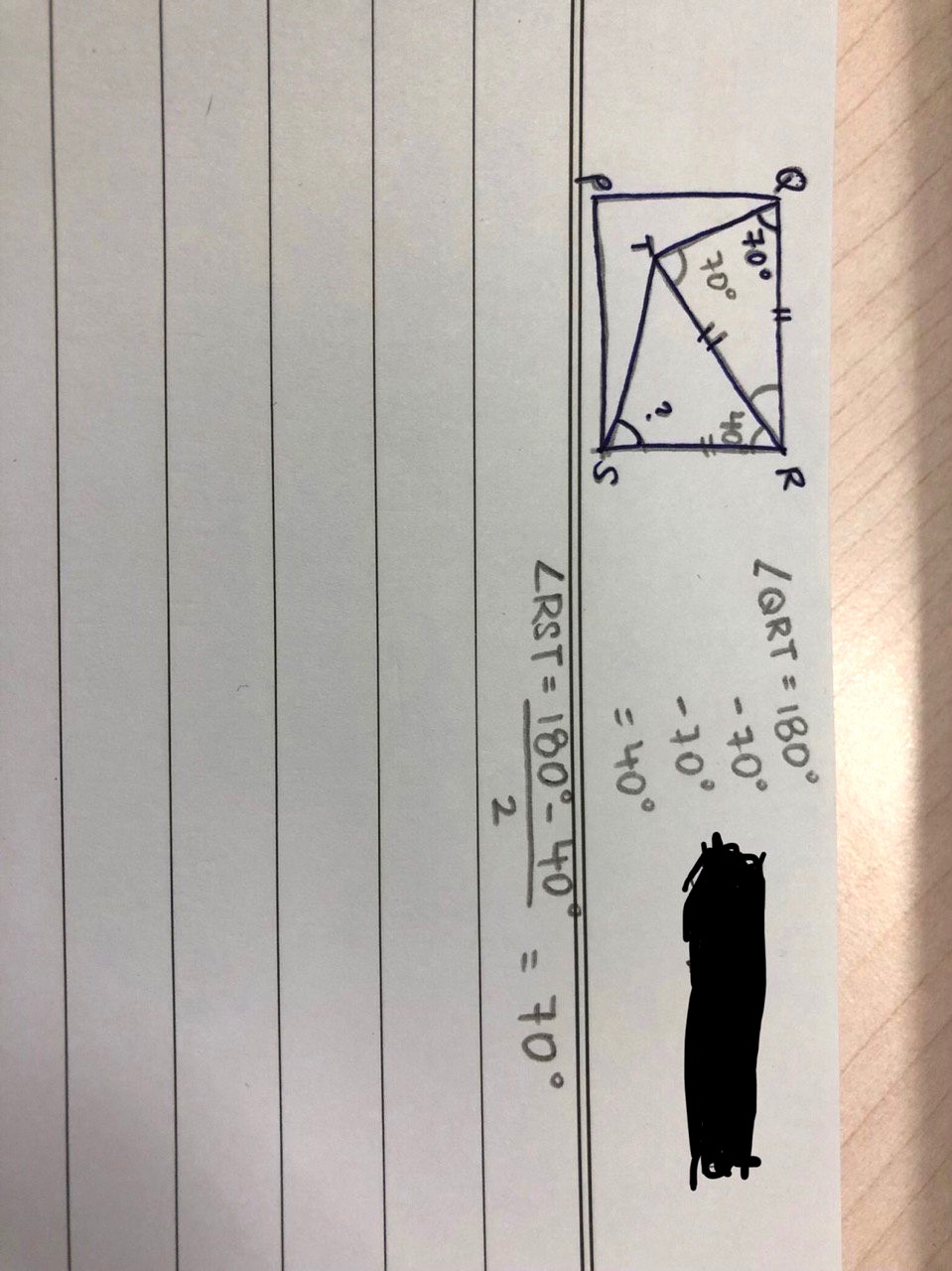


Angle TRS cannot be 40° as the sum of angle TRS and angle QRT (which gives QRS) would then be 80°, but QRS is actually a right angle (90°), which is a contradiction.
angle TRS = angle QRS - angle QRT
= 90° - 40°
= 50°
Angle RST = (180° - 50°)/2 = 65°