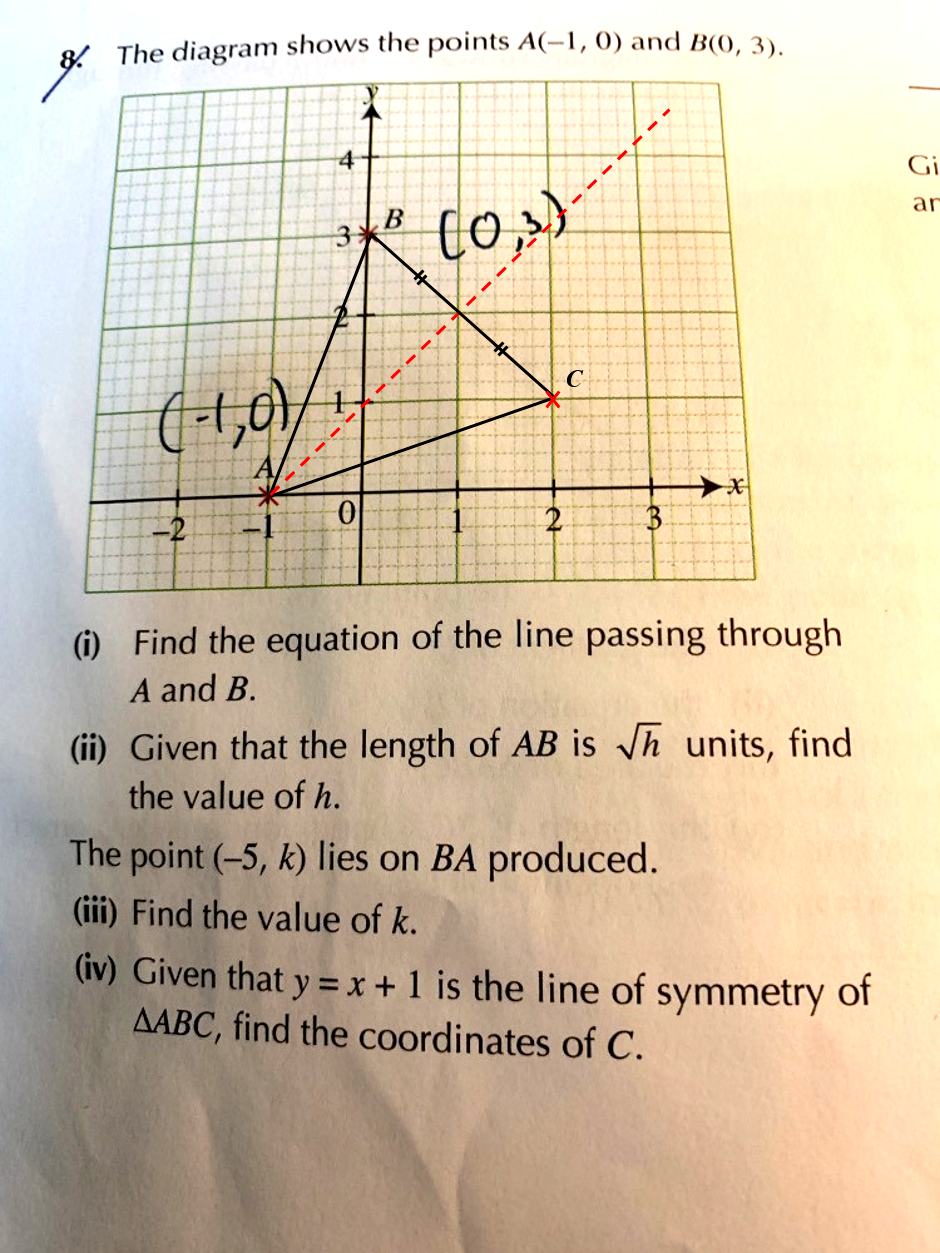
Whenever you're given such a question, first mark out the x and y-intercepts (and any other convenient points) of the new line. By substituting x=0 and y=0 we know that the line passes through A(-1,0) and (0,1). Since this is the line of symmetry of the triangle, it implies that it is the perpendicular bisector of the line segment BC. This means that points B and C are equidistant from the line. By observation, we see that B is 1 "big square" away from the line. C must therefore be the "mirror reflection" of B about the line.