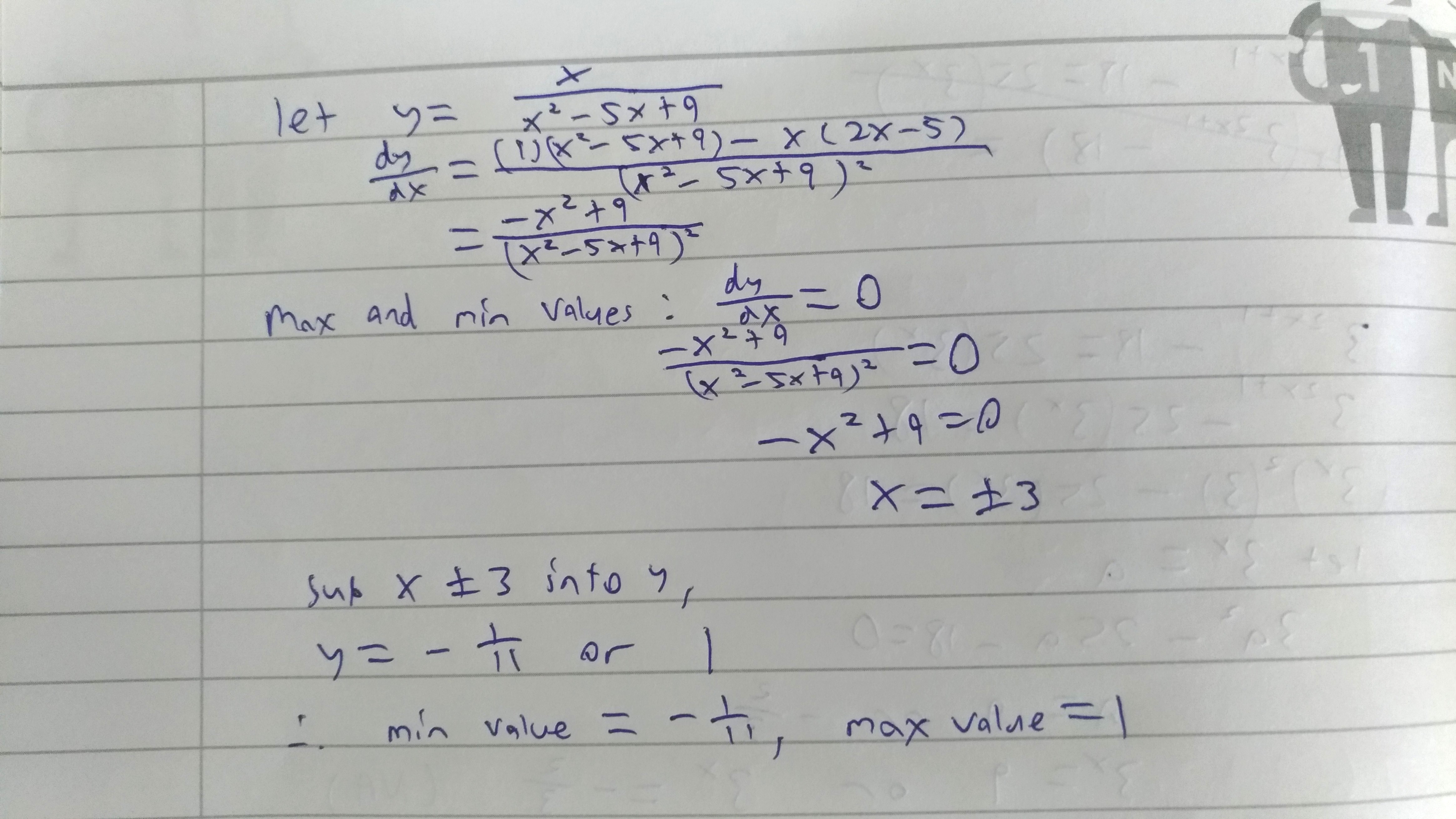Christmas MT's answer to Walking's Junior College 2 H1 Maths question.
Can I use number line?
If use number line have to trial and error. Using calculus can find the precise turning point
Turning points prove real roots?
Turning points mean maximum and minimum value
But how to show x is real
Solutions to turning points are values of x where max and min point occur
Don't need to prove x is real. It is assumed to be real in the question.
So the qns is something like " If x is real, find max and min value of the expression"
Why
Aaaa
I am so confuse
Cos x is always more than min value; or less than max value. By finding the min and max and i can prove the inequality
Min and max values can be found by equating its dy/dx = 0.
The easiest way is to plot the graph of the expression. There u can see the max and min point
What you've found is the local min/max which may not be the absolute min/max. I think you need to further show that it tends to a certain value as x tends to ±∞.
And I think the qn has an error, it should include equality, ie ≤ and ≥
And I think the qn has an error, it should include equality, ie ≤ and ≥
I also think the question's inequility signs are wrong. And there's a non-calculus proof presented in Answer 2.