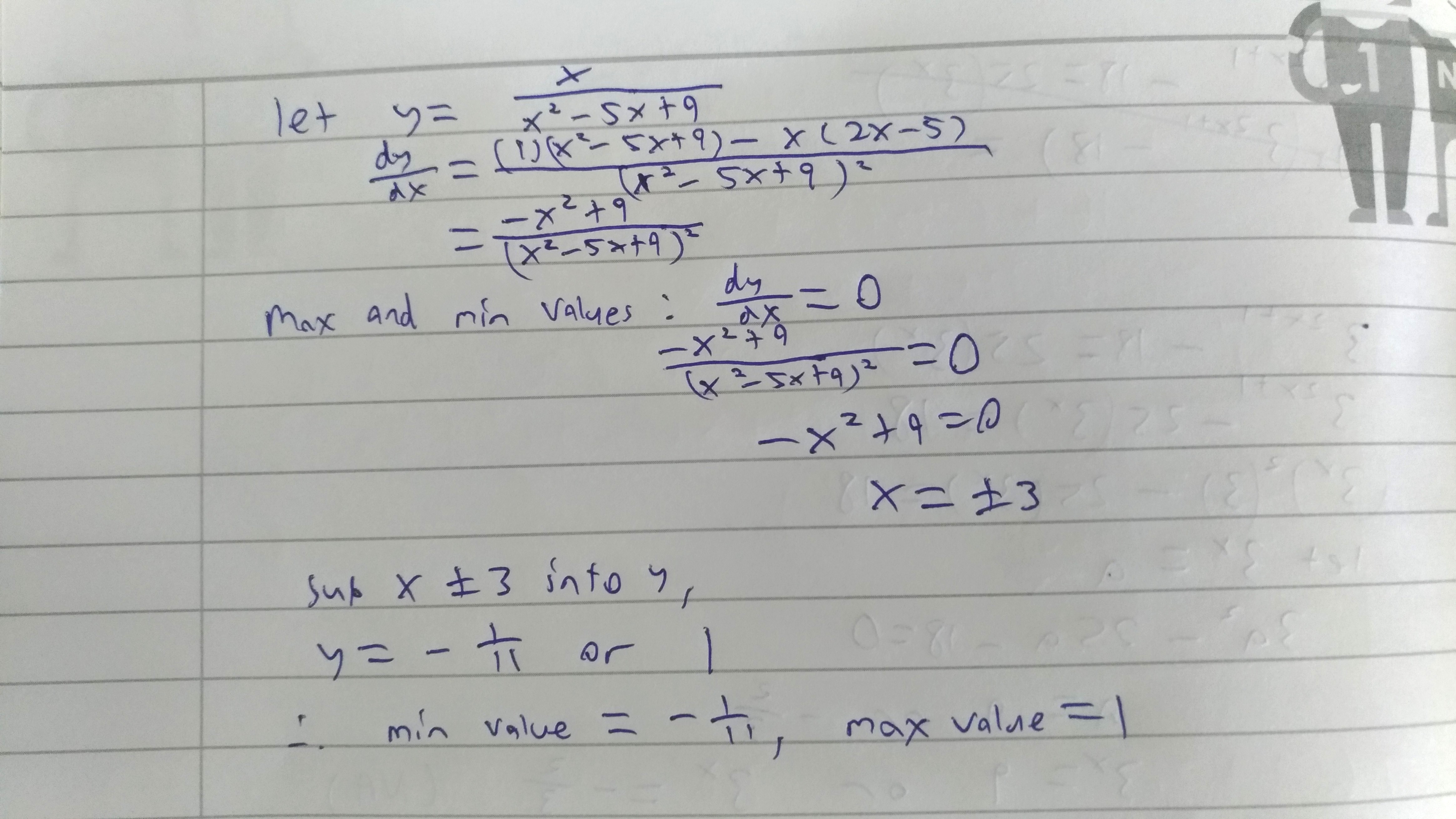Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
junior college 2 | H1 Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.
Hi does anyone knows how to solve this?
Date Posted: 6 years ago
Views: 608
See 2 Answers
Can I use number line?
If use number line have to trial and error. Using calculus can find the precise turning point
Turning points prove real roots?
Turning points mean maximum and minimum value
But how to show x is real
Solutions to turning points are values of x where max and min point occur
Don't need to prove x is real. It is assumed to be real in the question.
So the qns is something like " If x is real, find max and min value of the expression"
Why
Aaaa
I am so confuse
Cos x is always more than min value; or less than max value. By finding the min and max and i can prove the inequality
Min and max values can be found by equating its dy/dx = 0.
The easiest way is to plot the graph of the expression. There u can see the max and min point
What you've found is the local min/max which may not be the absolute min/max. I think you need to further show that it tends to a certain value as x tends to ±∞.
And I think the qn has an error, it should include equality, ie ≤ and ≥
And I think the qn has an error, it should include equality, ie ≤ and ≥
I also think the question's inequility signs are wrong. And there's a non-calculus proof presented in Answer 2.
Hmmmm I think you got the qn upside down. The qn is if x is real then prove the inequality. Not given the given the inequality, prove that x is real.
Hmm.. i think you didn't follow my reasoning and conclusion. :)
Note the double implication i used on each step, and in the end i mentioned "implying backwards".
Note the double implication i used on each step, and in the end i mentioned "implying backwards".
I mean can you start off like that and do the "double implication". Issit legit?
The question is.. Is the logic Of the proof sound And correct?
A <=> B <=> C <=> D
Hence D => A
Correct?
A <=> B <=> C <=> D
Hence D => A
Correct?
Yeap I get your logic but I just thought given the way the qn is asked, direct proofs make more sense ie, start with -(x-3)²≤0≤11(x+3)²
Instead of going by your way of "indirect" proof I suppose? I'm not sure actually, I'm not a math major :/
Instead of going by your way of "indirect" proof I suppose? I'm not sure actually, I'm not a math major :/
But in the first place, how woud you know to start with -(X-3)² ≤ 0 ≤ 11(x+3)² ?
So your "direct approach" is merely working backwards.
Neither am i a math major.. ;)
So your "direct approach" is merely working backwards.
Neither am i a math major.. ;)
I didn't get it...
Wow why can you add the equal there
What is the meaning of implying backwards
qn meaning?
A B C D there I didn't get it too...
Yeap work backwards. This is akin to finding the epsilon when doing limits problems. They begin with some rough work and then start the actual proof by working backwards from there. I mean your logic is fine, it's just the presentation seems awkward to me :/
Maybe we should stick to calculus hahaha
Maybe we should stick to calculus hahaha
360 Tutoring Program