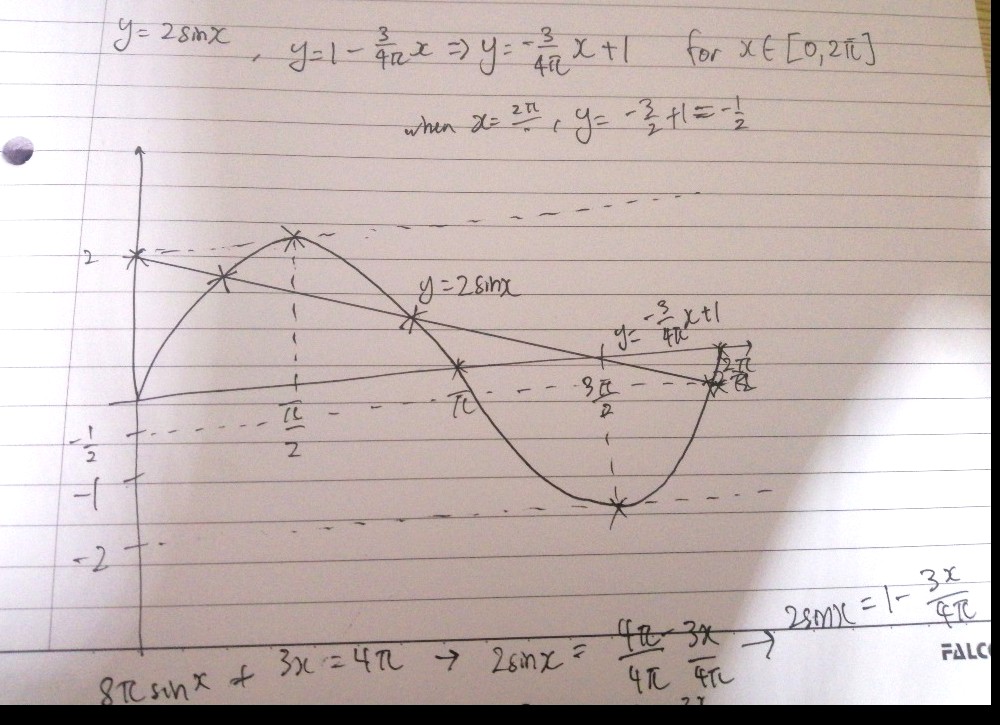
2sinx has a period of 2pi and an amplitude of 2. So it reaches maximum, 2, when x = pi/2, and reaches minimum, - 2, when x = 3pi/2. And 2sinx = 0 when x = 0, pi and 2 pi.

For the line, only need 2 points to draw, so when x =0, y = 1, and when x = 2pi, y = - 1/2. And just plot these 2 points.

For the last equation given, it can be manipulated to 2sinx on one side, and 1- 3x/4pi on the other. And notice they are equal at the points of intersection (as seen on the graph i just drew). Since there are 3 intersection points, there are 3 solutions.