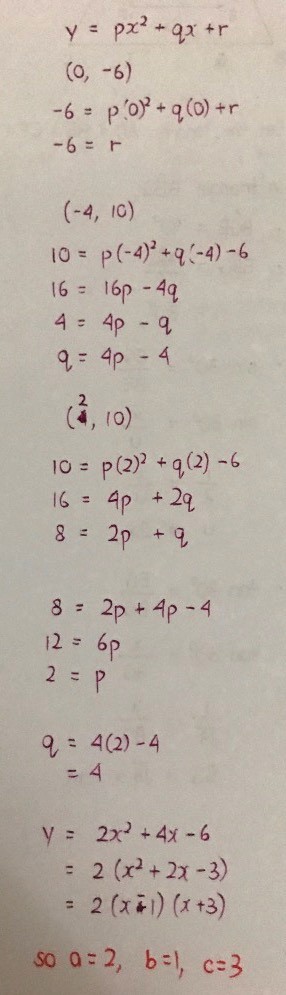Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
secondary 4 | E Maths
3 Answers Below
Anyone can contribute an answer, even non-tutors.
Help to solve
Date Posted: 4 years ago
Views: 213
Wait
See 3 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
One possible approach. The other is plain substitution of
1. x = -4, y = 10
2. x = 0, y = -6
3. x = 2, y = 10
into the equation and solving simuls as wel.
1. x = -4, y = 10
2. x = 0, y = -6
3. x = 2, y = 10
into the equation and solving simuls as wel.
Date Posted:
4 years ago
Thank you sir
For this one I recommend you to use the format ax2 + bx + c instead of the given equation. Else three simuls in three unknowns is going to be tedious to solve.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Hi, I provide 1 to 1 tuition, $40/1.5h, can cover English / Maths / Science, ex-school teacher with more than 20 years of teaching experience, can produce teaching cert from NIE, WhatsApp 9033 8810 or email [email protected] :)
Date Posted:
3 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
This should be easier to understand
Date Posted:
4 years ago
Yes second one is easy
To add,
There are three formats to consider.
1. y = ax² + bx + c
2. y = a (x + b) (x + c)
3. y = a (x + h)^2 + k
Which is the best approach to use, or are there times where one approach is preferred?
---------------------------------------------
1. y = ax² + bx + c
This approach is preferred when the y-intercept of the graph is provided and two other points on the curve are provided, as is the case in this question.
If (0, -6) is a point on the curve, then c = -6.
We use the other two points (-4, 10) and (2, 10) to form two simuls in two unknowns and solve.
---------------------------------------------
2. y = a (x + b) (x + c)
This approach is preferred when the TWO x-intercepts are provided and one more point is provided.
Suppose the x-intercepts are -3 and 1. Then we have y = a (x + 3) (x - 1). We use the third coordinate to obtain the value of a.
---------------------------------------------
3. y = a (x + h)^2 + k
This approach is preferred when the turning point of the curve is provided and one other point is provided.
If the turning point of the curve is (-1, -8), then by default, h = 1 and k = -8.
Now we have one unknown a left, and we just need one other coordinate (0, -6) to obtain the value of a.
There are three formats to consider.
1. y = ax² + bx + c
2. y = a (x + b) (x + c)
3. y = a (x + h)^2 + k
Which is the best approach to use, or are there times where one approach is preferred?
---------------------------------------------
1. y = ax² + bx + c
This approach is preferred when the y-intercept of the graph is provided and two other points on the curve are provided, as is the case in this question.
If (0, -6) is a point on the curve, then c = -6.
We use the other two points (-4, 10) and (2, 10) to form two simuls in two unknowns and solve.
---------------------------------------------
2. y = a (x + b) (x + c)
This approach is preferred when the TWO x-intercepts are provided and one more point is provided.
Suppose the x-intercepts are -3 and 1. Then we have y = a (x + 3) (x - 1). We use the third coordinate to obtain the value of a.
---------------------------------------------
3. y = a (x + h)^2 + k
This approach is preferred when the turning point of the curve is provided and one other point is provided.
If the turning point of the curve is (-1, -8), then by default, h = 1 and k = -8.
Now we have one unknown a left, and we just need one other coordinate (0, -6) to obtain the value of a.
Take note of these as it simplifies your workings greatly.
Thank you for going the extra mile to help me out. Thank you so mucb
360 Tutoring Program