Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

i dont to do do and sketch the graph
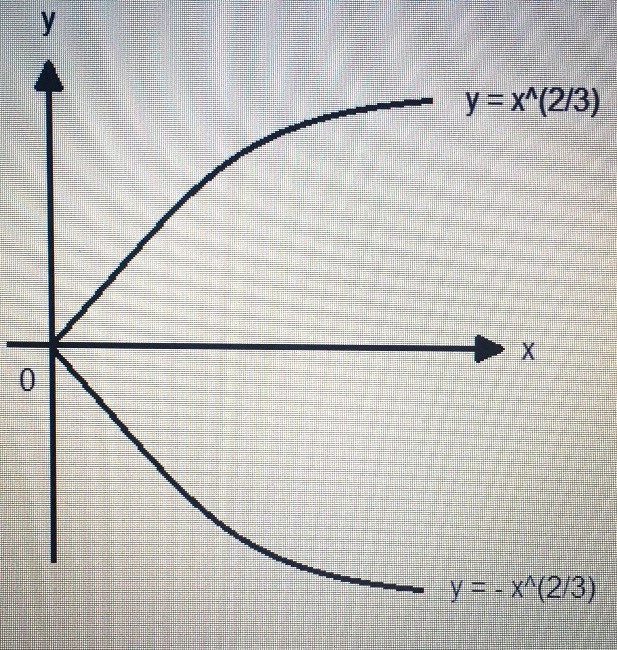
For the graph of y = -x^2/3, we just reflect that graph along the x-axis.
See 2 Answers
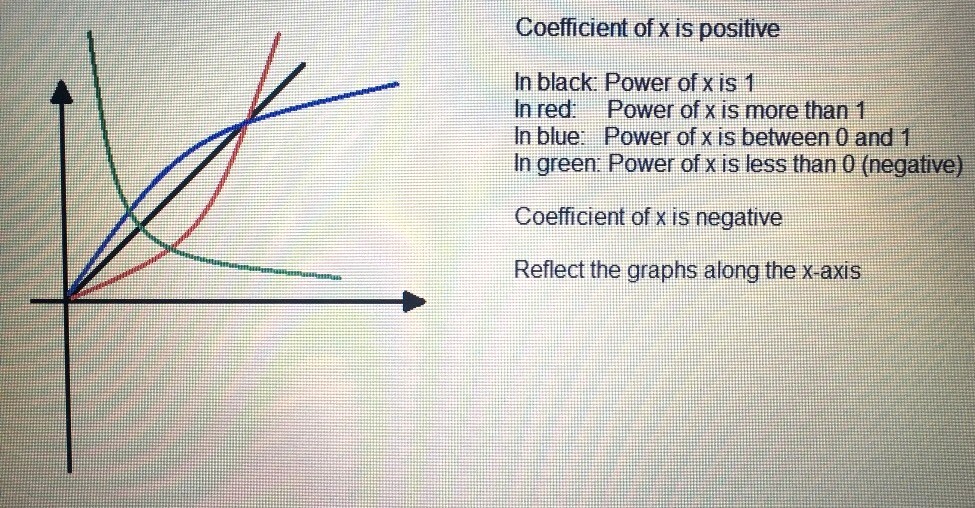
If the power of x is 1, the graph is linear (this is in E Maths, but I put this for comparison purposes).
If the power of x is more than 1, the graph starts slow first but then suddenly curves upwards very quickly. This is because as x increases, y increases rapidly (think of y = x2).
Similar logic applies for power of x from 0 to 1. The graph starts moderately fast at first but then slows down. This is because as x increases, y no longer increases by much.
For the last case where the power of x is negative, the graph goes down in the manner I have drawn. This is because as x increases, y decreases, yet the value of y can never be negative. As x increases, t decreases but the rate of decrease slows down (think of y = 1/x from E Maths).
Let me know if you need more explanation on this and I will do my best to explain again.