Hi, I provide 1 to 1 tuition, $10/1.5h, can cover English / Maths / Science, ex-school teacher, can produce teaching cert from NIE, WhatsApp 9033 8810 or email [email protected] :)

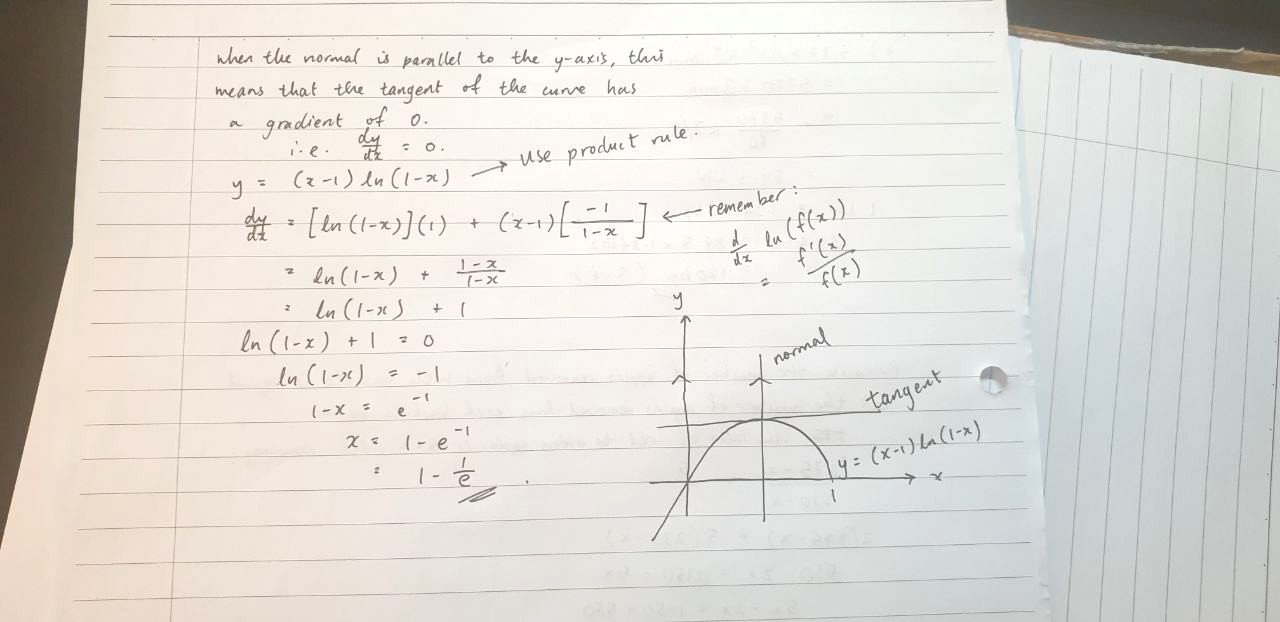
This question seems challenging at first, but once you understand what the condition really means, you will be able to solve it very quickly.

As a visualisation, I have sketched out the positive x and y axes and the graph of y = (x - 1) ln (1 - x). The graph is an increasing function for x < 0, so this is the only point where the normal to the graph is parallel to the y-axis. Do not worry about what the graph looks like because you are not required by the A-Math syllabus to know the appearance or shape of this graph. As you can see, when the normal to the graph is parallel to the y-axis, this means that the tangent to the graph is parallel to the x-axis (i.e. dy/dx = 0).

Find dy/dx using the product rule. Recall the differentiation of logarithmic functions as well. Solve for x and leave the answer in exact terms.