Why 5U for the Green ballons? I thought should be 1 unit for 3/4 burst and left 1 unit.tks

Hi, Sin Yee, i think i knew why 4u and 5u . 4u of 5 =20 and 5u of 4= 20 . Tks so much

The method is correct. But it’s tough to break down the model here.

The model for Red balloons should be redrawn as such :

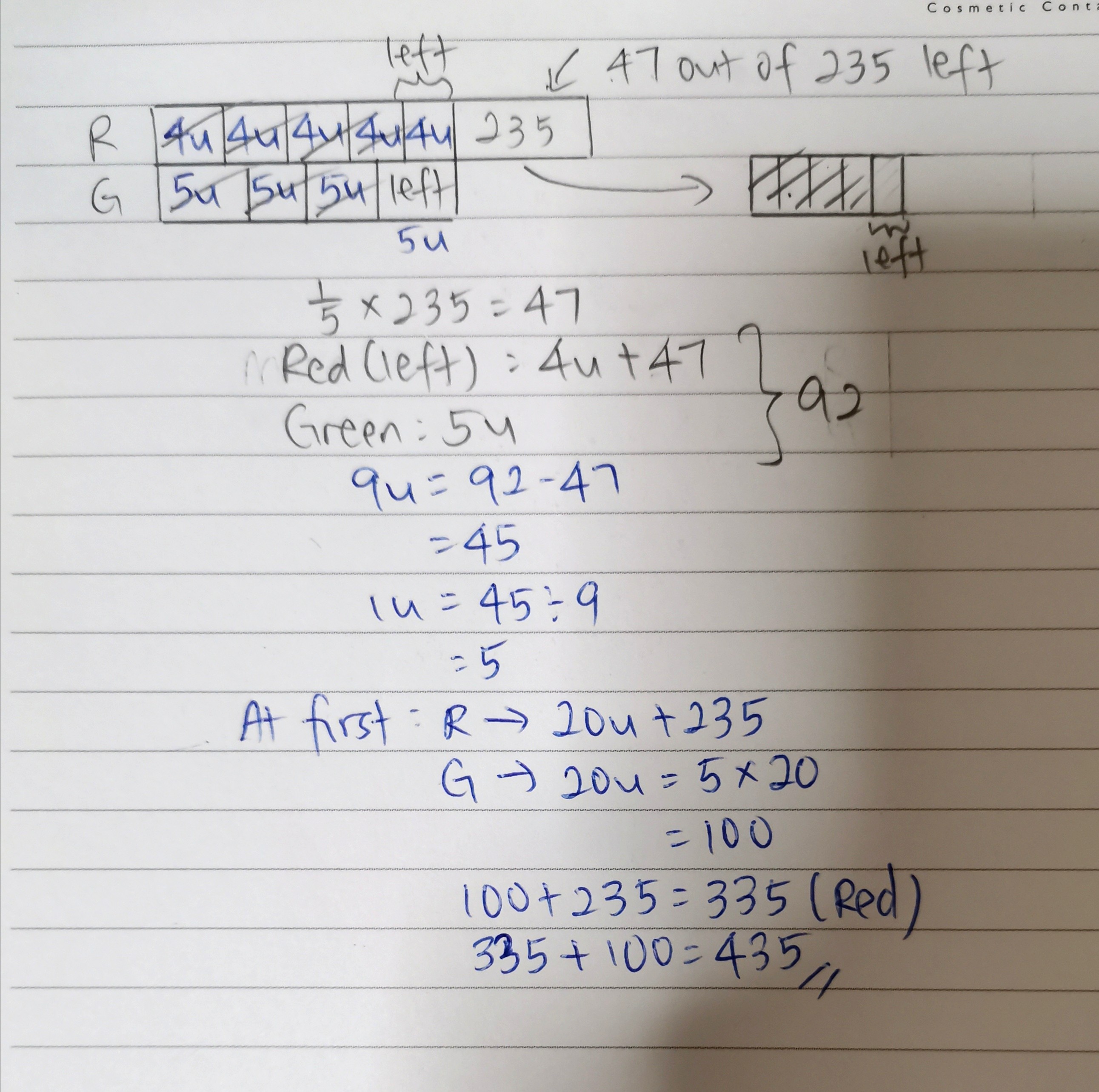
⬛ Represents 4u


R ⬛47 ⬛47 ⬛47 ⬛47 ⬛47

As we can see, R still equals 20u + 235 but we have redrawn it into 5 equal parts of 4u + 47.

The basis behind using 20u (4 x 5) is that 20 is the lowest common multiple of 4 and 5, so using it allows exact division by both 5 and 4.

Of course , you may choose to use other higher common multiples as well.

Using 20u for green and 20u + 235 for red allows us to compare them easily, since the units are of the same size/value/quantity.


After 4/5 of red were burst and 3/4 of green were burst,

1/5 of red were left and 1/4 of green were left

1/4 of green : 20u ÷ 4 = 5u
1/5 of red : (20u + 235) ÷ 5 = 4u + 47


Total left over = 5u + 4u + 47 = 9u + 47

This is equal to 92.

So 9u = 92 - 47 = 45
1u (or simply written as u, the 1 is optional) = 45 ÷ 9 = 5



Total Balloons at first = 20u + 20u + 235
= 40u + 235
= 40 × 5 + 235
= 200 + 235
= 435

Sin Yee's model is easily understandable provided the concept below is clear to the student :

Sum(or summation) of the same fraction of individual parts that make up the total = same fraction of total


Eg. 1/5 of 20u + 1/5 of 235 = 1/5 of all the red balloons

Eg. 1/3 × 9 = 3

But 9 = 6 + 3

1/3 × 6 + 1/3 × 3 = 2 + 1 = 3 = 1/3 × 9

so we can say 1/3 × 9 = 1/3 × (6 + 3) = 1/3 × 6 + 1/3 × 3

This is basically the distributive law of multiplication.

Ty