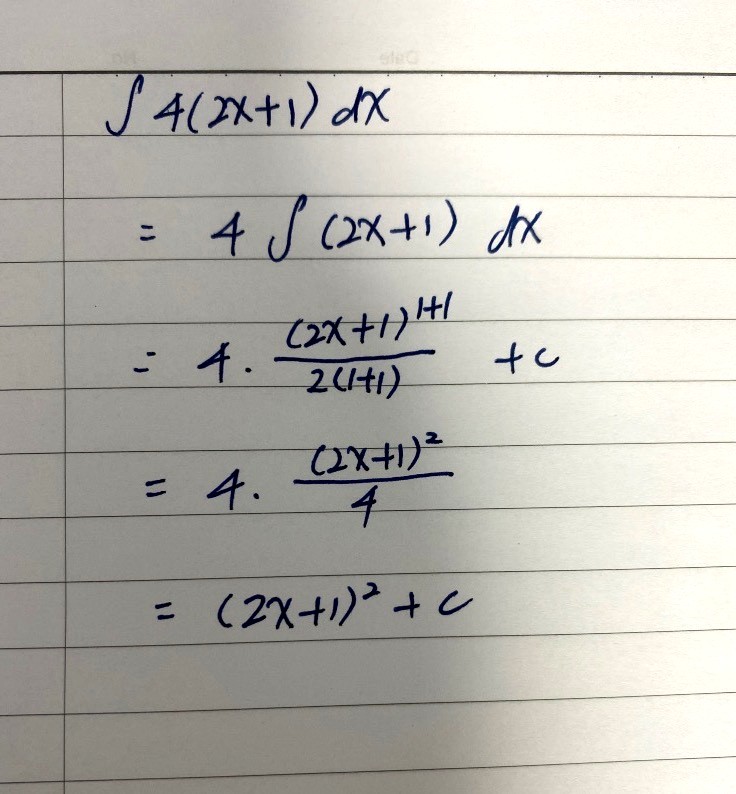QN's answer to QN's Junior College 2 H1 Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes

Can I do it this way?
Date Posted:
4 years ago
With u= ax+b apply chain rule. dy/dx=d/dx((ax+b)^n+1/a(n+1)+c)=(ax+b)^n So in integration, we reverse the process. That's what you have done. However when n=1, you integrate by applying linearity which means integrating individually only. You cannot put it as one term and integrate by using counter chain rule.
I will give you another example, integral 4 dx, you don't treat 4 as one whole term and say that integral (4)^1dx, where f(x)=4 f'(x)=0 . Because if you are to do that, it will be (4)^2/(0*2) +c which isn't valid. Instead integral 4dx = 4x +c. Because the (ax+b) in that case don't come together, so it's actually not really (ax+b)^1.
So I can only use that formula when n ≠ 0,-1, and 1?
You have to know why and try to prove it. When n=-1, it's a ln graph after integrating. When n=0, it's 1( anything power of 0 is 1). When n=1, it's just a variable and a constant in that expression. Yea, you may memorize in a way where n not equal to -1,0and 1. But most importantly you have to know why. Correct, in conclusion you can say that you can only use the formula when n is not the following values as mentioned unless proven otherwise. (ax+b)^n means ax+b is together (imagine it like a packet). When n =1, the terms are actually separated.
Okok I understand what you mean. The terms are separated so I need to integrate differently and not combine as a set.
In this case it would be 4.∫2x dx + ∫1x^0 dx
thanks for explaining!
If you differentiate (ax+b)^2, it gives you 2(ax+b)*a. That means (ax+b) is together, in indices law you call it the power base. However, if you differentiate ax^2 +bx, it gives the same result but ax^2+bx is not the same as (ax+b)^2.
In this case it would be 4.∫2x dx + ∫1x^0 dx - yep you are correct. Or you may present in this way too 8∫x dx + ∫1x^0 dx or any identical way you are comfortable with.
When I differentiate d/dx(ax+b)^2 I get 2a(ax+b).
And differentiate ax^2+bx gives 2ax+b.
So the difference lies in the different answer from both equations?
And differentiate ax^2+bx gives 2ax+b.
So the difference lies in the different answer from both equations?
I typed abit wrongly, I mean both may give the same result. However it is different as we cannot treat (ax+b ) to be the base of power of 1.
You may try expanding (2x+1)^2 and compare with 4x^2+4x
d/dx (2x + 1)²
= 2(2x + 1)(2)
= 4(2x + 1)
d/dx (4x² + 4x)
= 4 d/dx (x² + x)
= 4 (2x + 1)
He was intending to say differentiating (ax + b)² vs differentiating a(ax² + 2bx)
The former expands to a²x² + 2abx + b². The latter expands to = a²x² + 2abx
The difference is in the constant.
= 2(2x + 1)(2)
= 4(2x + 1)
d/dx (4x² + 4x)
= 4 d/dx (x² + x)
= 4 (2x + 1)
He was intending to say differentiating (ax + b)² vs differentiating a(ax² + 2bx)
The former expands to a²x² + 2abx + b². The latter expands to = a²x² + 2abx
The difference is in the constant.
I understand. Thank you!:)