See Ignatius Yeo's answer to QN's Junior College 2 H1 Maths Singapore question

Ignatius Yeo's answer to QN's Junior College 2 H1 Maths Singapore question.

1 Upvotes

0 Downvotes

The picture shows 2 methods of doing it - product rule and chain rule. For chain rule, let f(x) be x^2+2. Differentiate f(x) and multiply e^f(x) as shown. Hope it helps!

Date Posted: 4 years ago

Comments 6 add a comment

4 years ago

Thanks, I get the second one!
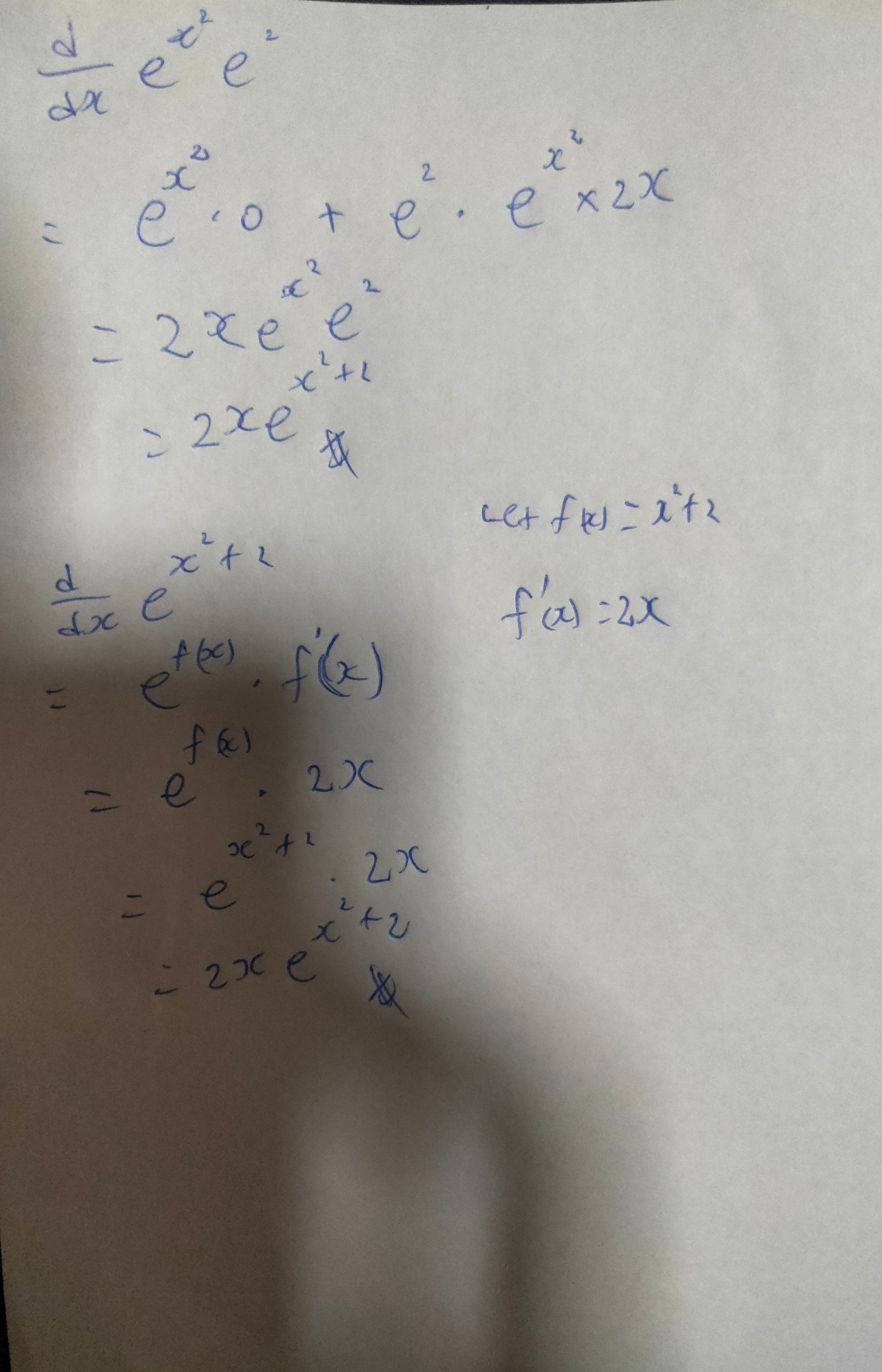
But the first one, why is e^x^2 when differentiated is e^x^2(0)?

Ignatius Yeo

4 years ago

Whenever you differentiate a constant value, it is 0. The first method is product rule. First term multiply by derivative of second term, and second term multiply derivative of first term. e^2 is a constant with no variables. Therefore d/dx e^2=0.

4 years ago

Product rule...

d/dx (e^(x²) e²)

= e^(x²) d/dx (e²) + (d/dx e^(x²) ) e²

= e^(x²) (0) + 2xe^(x²) (e²)

= 2xe²e^(x²)

= 2x e^(x²+2)

Remember that differentiating a constant gives 0

Ignatius Yeo

4 years ago

Another tip d/dx e^2 = d/dx e^2(x^0). Applying differentiation rule, d/dx (e^2(x^0))= 0*x^-1*e^2=0. Anything multiplies 0 is always 0. Hence, d/dx constant =0.

4 years ago

Thanks a lot!!

Ignatius Yeo

4 years ago

You're welcome.