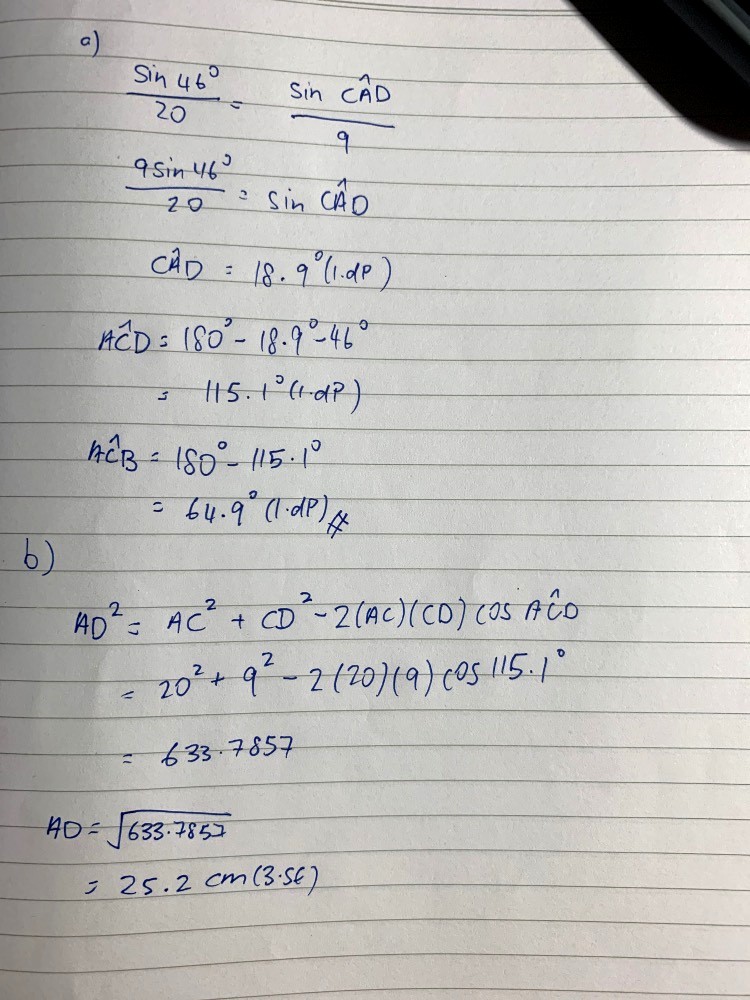A math god's answer to LockB's Secondary 3 A Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes

For part (a) use sin rule to find angle CAD. Because some of angles in a triangle= 180. U are able to find angle ACD. After that can take 180- angle ACD to find angle ACB because it is a straight line.
For part (b) use cos rule to find length AD.
For part (b) use cos rule to find length AD.
Date Posted:
4 years ago
LockB, do note one pitfall in using the sine rule. Remember that sin (180 - x) = sin x rule? So let’s say sin 150 = sin 30 = 1/2. You wish to find angles such that sin x = 1/2. Note that x can be an acute or an obtuse angle (for the case of sin), so take this into account.
For this particular triangle, we need to be wary of that possibility, because as you obtain sin CAD = number, as per what I explained above, CAD can either be the acute angle sin-1 (number) or 180 minus this acute angle.
Fortunately, from the other triangle, we know that angle ACB is acute, so the accompanying angle ACD must be obtuse. Hence, CAD must be an acute angle and we can safely extract the acute value for angle CAD.
For this particular triangle, we need to be wary of that possibility, because as you obtain sin CAD = number, as per what I explained above, CAD can either be the acute angle sin-1 (number) or 180 minus this acute angle.
Fortunately, from the other triangle, we know that angle ACB is acute, so the accompanying angle ACD must be obtuse. Hence, CAD must be an acute angle and we can safely extract the acute value for angle CAD.
thx :)