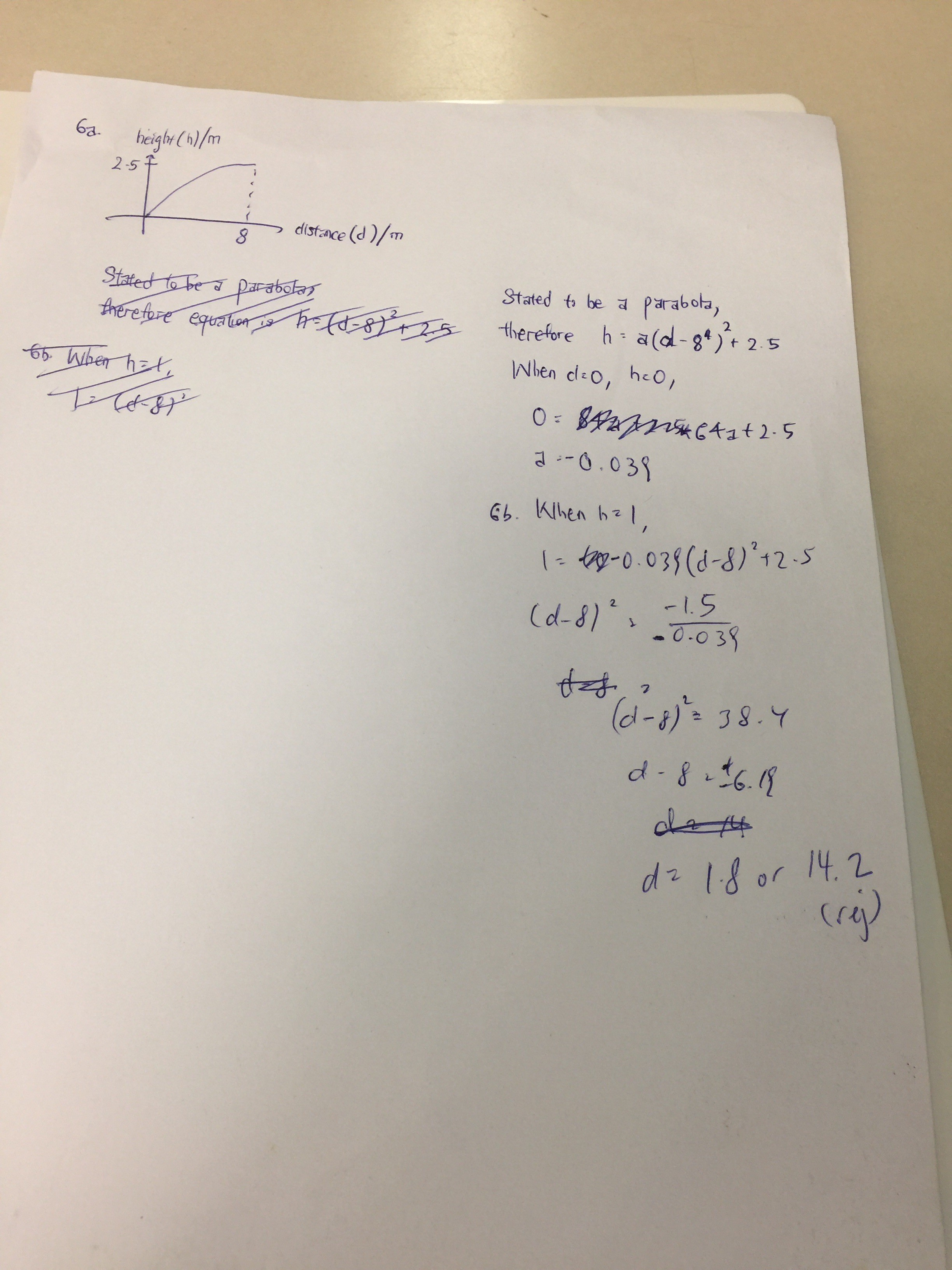Christmas MT's answer to MoeSatt Hmon's Junior College 1 H1 Maths question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes

Sorry for the mess. Made a few careless mistakes.
It's stated to be a parabola, meaning the function is quadratic. The maximum was stated to be (8 , 2.5), therefore we know the equation is in the form y = a (x-8)^2 + 2.5 and a is negative (recall this from the "complete the square" chapter in... Sec 3?)
To find a, all we have to do is to sub (0,0) into the equation (why the curve has to pass through (0,0) should be obvious enough).
The rest is just "sub numbers into formula".
It's stated to be a parabola, meaning the function is quadratic. The maximum was stated to be (8 , 2.5), therefore we know the equation is in the form y = a (x-8)^2 + 2.5 and a is negative (recall this from the "complete the square" chapter in... Sec 3?)
To find a, all we have to do is to sub (0,0) into the equation (why the curve has to pass through (0,0) should be obvious enough).
The rest is just "sub numbers into formula".
Date Posted:
7 years ago
why the answer 14.2 is rejected?and in the equation h=a(d-8)^2+2.5 why it is -8
isn't it follow the format h=a(x+b)^2+c?
isn't it follow the format h=a(x+b)^2+c?
The format is actually y = a (x-b)^2 + c to have a turning point at (b,c).
As for why 14.2 was rejected, it's because I'm an idiot. Somehow subconsciously thought I was only supposed to draw the function only up to the turning point. Looks like the mistakes were more than just "a few".
Sorry about those. Please draw a complete n-shape parabola and don't reject 14.2.
As for why 14.2 was rejected, it's because I'm an idiot. Somehow subconsciously thought I was only supposed to draw the function only up to the turning point. Looks like the mistakes were more than just "a few".
Sorry about those. Please draw a complete n-shape parabola and don't reject 14.2.
oh i see thank you u r so wise