Christmas MT's answer to GK's Junior College 1 H3 Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes

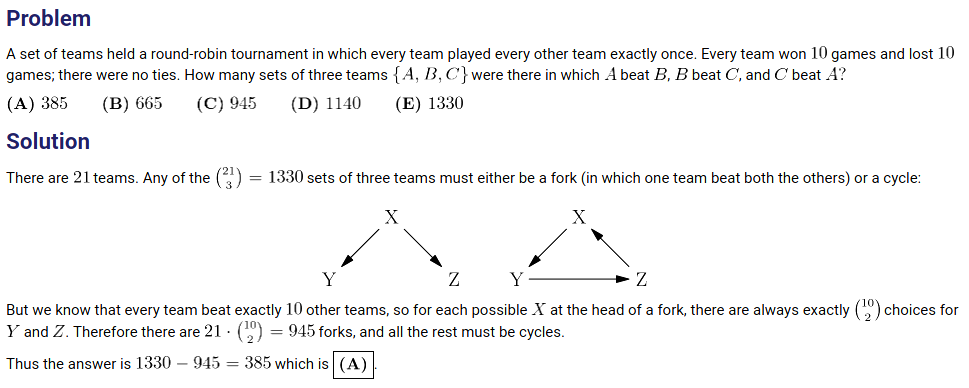
I think this is the answer you were looking at? Image courtesy of Art of Problem Solving, a very cool math website. I'll just elaborate more on the given solution.
Consider Team 1. We were told that each team wins 10 times, loses 10 times, and never gets a draw. Hence, team 1 must have played 20 times. Also, since team 1 plays with each of team 2, team 3, etc. only once, there must be 20 other teams aside from team 1 in order for team 1 to play 20 times. Together, there are thus 21 teams.
We are considering a set of three teams out of 21 teams. Because order within this set does not matter, we are looking at 21C3 sets of three teams i.e. 1330 sets of teams.
Now we consider the play dynamics within a set of three teams. Consider the set consisting of team X, team Y, and team Z. Team X plays against Y and Z each exactly once. Thus, either X wins twice or X wins once and loses once or X loses twice. For every team that wins twice, there must be another team that loses twice. For example, if X wins against both Y and Z, that means Y lost once and Z lost once. Y then plays against Z. If Y wins, then Z would have lost twice in total. Similarly, if Z wins, then Y would have lost twice in total.
Without loss of generality, we assume either X wins twice or X wins once and loses once. We can do this because even if X loses twice, there must be a team that wins twice and we shall just rename that team as X. Using the terminology in the answer, we name the scenario where X wins twice as a fork and where X wins once and loses once as a cycle. The latter scenario is named a cycle because by saying X won once and lost once, we also imply that Y and Z both also won once and lost once. If not, then there is a team that won twice, which is the fork scenario.
Next, we consider a fork containing X, with X beating two teams. We also know that X have beaten 10 other teams as given in the question. Hence, there are 10C2 ways of constructing such forks i.e. there are 45 such forks. For example, say X has beaten A, B, C, ..., J. Then, {X, A, B} is a fork, and so is {X, A, C} and {X, B, J}. We can thus choose 2 out of 10 to form a fork i.e. there are 45 forks.
There are a total of 21 teams that could be X i.e. 21 * 45 = 945 sets of three teams where one team beats two other teams.
We established earlier that there are a total of 1330 sets of three teams, and a set of three teams is either a fork or a cycle. Since there are 945 sets out of 1330 which is denoted as a fork, then there must be 1330 - 945 = 385 sets (Q.E.D)
Consider Team 1. We were told that each team wins 10 times, loses 10 times, and never gets a draw. Hence, team 1 must have played 20 times. Also, since team 1 plays with each of team 2, team 3, etc. only once, there must be 20 other teams aside from team 1 in order for team 1 to play 20 times. Together, there are thus 21 teams.
We are considering a set of three teams out of 21 teams. Because order within this set does not matter, we are looking at 21C3 sets of three teams i.e. 1330 sets of teams.
Now we consider the play dynamics within a set of three teams. Consider the set consisting of team X, team Y, and team Z. Team X plays against Y and Z each exactly once. Thus, either X wins twice or X wins once and loses once or X loses twice. For every team that wins twice, there must be another team that loses twice. For example, if X wins against both Y and Z, that means Y lost once and Z lost once. Y then plays against Z. If Y wins, then Z would have lost twice in total. Similarly, if Z wins, then Y would have lost twice in total.
Without loss of generality, we assume either X wins twice or X wins once and loses once. We can do this because even if X loses twice, there must be a team that wins twice and we shall just rename that team as X. Using the terminology in the answer, we name the scenario where X wins twice as a fork and where X wins once and loses once as a cycle. The latter scenario is named a cycle because by saying X won once and lost once, we also imply that Y and Z both also won once and lost once. If not, then there is a team that won twice, which is the fork scenario.
Next, we consider a fork containing X, with X beating two teams. We also know that X have beaten 10 other teams as given in the question. Hence, there are 10C2 ways of constructing such forks i.e. there are 45 such forks. For example, say X has beaten A, B, C, ..., J. Then, {X, A, B} is a fork, and so is {X, A, C} and {X, B, J}. We can thus choose 2 out of 10 to form a fork i.e. there are 45 forks.
There are a total of 21 teams that could be X i.e. 21 * 45 = 945 sets of three teams where one team beats two other teams.
We established earlier that there are a total of 1330 sets of three teams, and a set of three teams is either a fork or a cycle. Since there are 945 sets out of 1330 which is denoted as a fork, then there must be 1330 - 945 = 385 sets (Q.E.D)
Date Posted:
5 years ago