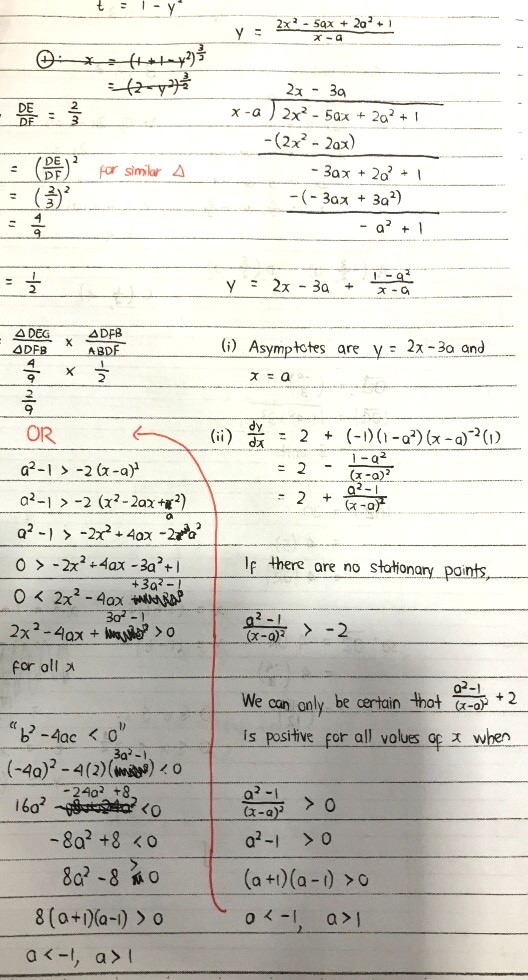Eric Nicholas K's answer to Rachel's Junior College 2 H2 Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Here. For my first reasoning in part ii, if the value of x in (x - a)^2 gets very close to a, and -1 < a < 1, then the fraction (a^2 - 1) / (x - a)^2 may get negative and this may cause dy/dx to become zero for a specific value of x.
Hence, the only way to be certain of no turning point is if the numerator is positive (the denominator is already positive).
Alternatively, we can use discriminant of roots to solve for a.
Hence, the only way to be certain of no turning point is if the numerator is positive (the denominator is already positive).
Alternatively, we can use discriminant of roots to solve for a.
Date Posted:
4 years ago
I’m starting to suspect that a = 1 or a = -1 is also accepted.
For a = 1, the equation for y reduces into
y = (2x^2 - 5x + 3) / (x - 1)
= (2x - 3) (x - 1) / (x - 1)
= 2x - 3
which has no turning points (except that the graph is not defined at x = 1).
Similarly, for a = -1,
y = (2x^2 + 5x + 3) / (x + 1)
= (2x + 3) (x + 1) / (x + 1)
= 2x + 3
which has no turning points (except that the graph is not defined at x = -1).
So both the +-1 cases are also accepted. Therefore, a <= -1 or a >= 1.
For a = 1, the equation for y reduces into
y = (2x^2 - 5x + 3) / (x - 1)
= (2x - 3) (x - 1) / (x - 1)
= 2x - 3
which has no turning points (except that the graph is not defined at x = 1).
Similarly, for a = -1,
y = (2x^2 + 5x + 3) / (x + 1)
= (2x + 3) (x + 1) / (x + 1)
= 2x + 3
which has no turning points (except that the graph is not defined at x = -1).
So both the +-1 cases are also accepted. Therefore, a <= -1 or a >= 1.