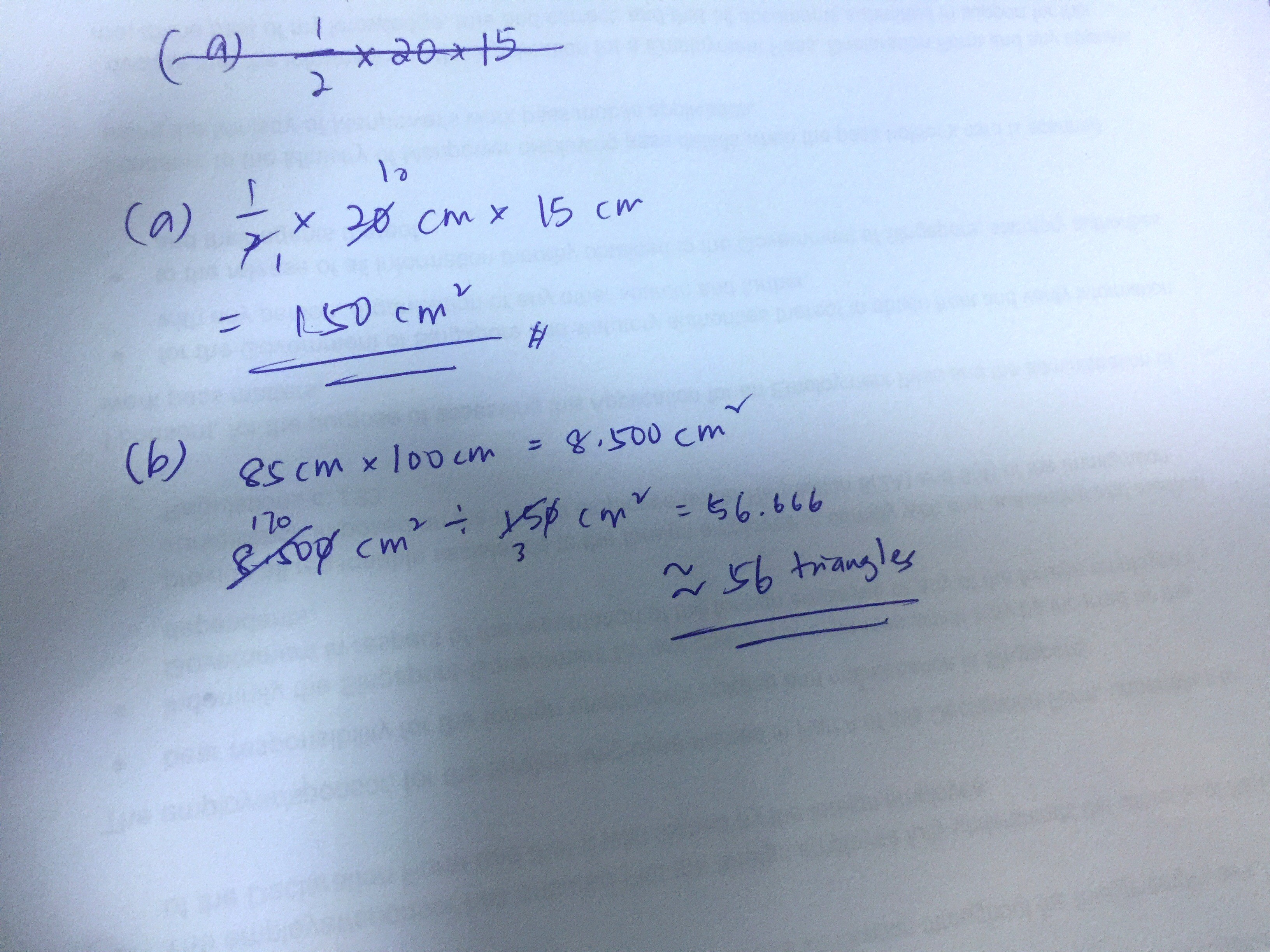Wong Siew Fang's answer to Jackyoggy's Primary 5 Maths Area & Volume Singapore question.
Your part b’s approach is flawed.
In such scenarios, we have to consider whether the triangles even fit the dimensions given. For example, how many squares of size 2 x 2 can we put inside a larger square of size 3 x 3?
Even though 9 is more than twice of 4, we cannot put two of those smaller squares inside, simply because the dimensions do not fit, and we are not allowed to cut the shape further to fill up the missing spaces. Hence, we can only put one such small square, and not two, inside the large square.
For this question, it’s a similar idea. I will consider the triangles in groups of two, forming a 15 x 20 rectangle.
The dimensions of the larger rectangle are 85 x 100.
There are two straightforward cases to this.
The first one is as follows. On the side of length 85, we fit as many 15s as possible and on the other side of length 100, we fit as many 20s as possible.
We realise that 85 divided by 15 is 5 (with remainder 10) and 100 divided by 20 is 5 (with no remainder), so the number of 15 x 20 rectangles we can put is 5 x 5 = 25, so the number of triangles we can put is 25 x 2 = 50.
The second is as follows. On the side of length 85, we fit as many 20s as possible and on the other side of length 100, we fit as many 15s as possible.
We realise that 85 divided by 20 is 4 (with remainder 5) and 100 divided by 15 is 6 (with remainder 10), so the number of 15 x 20 rectangles we can put is 4 x 6 = 24, so the number of triangles we can put is 24 x 2 = 48.
Other orientations will probably not get us any further triangles.
So, the largest number of triangles we can put in is 50, and not 56.
In such scenarios, we have to consider whether the triangles even fit the dimensions given. For example, how many squares of size 2 x 2 can we put inside a larger square of size 3 x 3?
Even though 9 is more than twice of 4, we cannot put two of those smaller squares inside, simply because the dimensions do not fit, and we are not allowed to cut the shape further to fill up the missing spaces. Hence, we can only put one such small square, and not two, inside the large square.
For this question, it’s a similar idea. I will consider the triangles in groups of two, forming a 15 x 20 rectangle.
The dimensions of the larger rectangle are 85 x 100.
There are two straightforward cases to this.
The first one is as follows. On the side of length 85, we fit as many 15s as possible and on the other side of length 100, we fit as many 20s as possible.
We realise that 85 divided by 15 is 5 (with remainder 10) and 100 divided by 20 is 5 (with no remainder), so the number of 15 x 20 rectangles we can put is 5 x 5 = 25, so the number of triangles we can put is 25 x 2 = 50.
The second is as follows. On the side of length 85, we fit as many 20s as possible and on the other side of length 100, we fit as many 15s as possible.
We realise that 85 divided by 20 is 4 (with remainder 5) and 100 divided by 15 is 6 (with remainder 10), so the number of 15 x 20 rectangles we can put is 4 x 6 = 24, so the number of triangles we can put is 24 x 2 = 48.
Other orientations will probably not get us any further triangles.
So, the largest number of triangles we can put in is 50, and not 56.