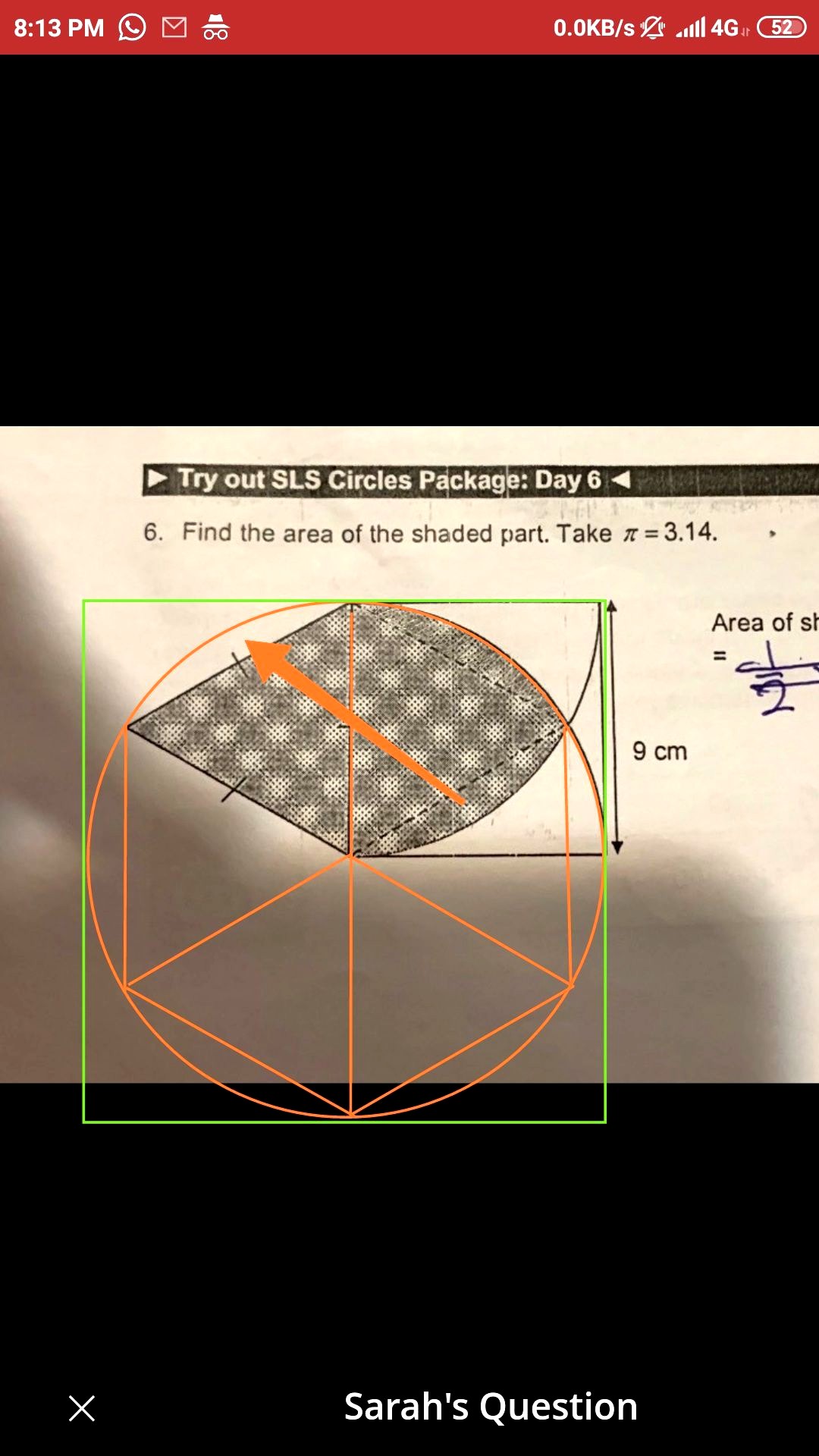
Can you see another sector below the first sector? The 9 cm line? Imagine it moved up and it will match the triangle . So both triangle's area is 40.5 .

You might want clarify which part you are shifting up. Because the area of the equilateral triangle isn't 40.5 no matter what you shift

Another way of calculating the area of the triangle without using Pythagoras' Theorem is ½ab sin c , where

a and b are the sides of the triangle, 9cm each.

c is the angle subtended by these two sides. It's 60° since it's an angle of an equilateral triangle.

½ x 9 x 9 sin60°
= ½ x 81 x √3/2
= 81/4 x √3
= 35.07 (4s.f)


Another way to see why it isn't 40.5 :

Take the line joining the two equilateral triangles as the base of the right equilateral triangle.

Its height would then be the horizontal line drawn from the middle of that line to the rightmost vertex.

Now this line is parallel to the horizontal sides of the square. However, it is shorter than them as shown in the diagram. Which means it is shorter than 9cm.

So the height of the triangle cannot be 9cm. And thus its area cannot be ½ x 9 x 9
and does not equal 40.5