See Eric Nicholas K's answer to Si En's Junior College 1 H2 Maths Singapore question

Eric Nicholas K's answer to Si En's Junior College 1 H2 Maths Singapore question.

1 Upvotes

0 Downvotes

First part

Here the sin y in -1/sin y comes as an “expression”, not an “equation”. Hence, when we express sin y in terms of cos y, there will not be a +- in front of the square root.

Date Posted: 5 years ago

Comments 3 add a comment

5 years ago

y = cos-1(x) has a restricted range of ［0,π ］

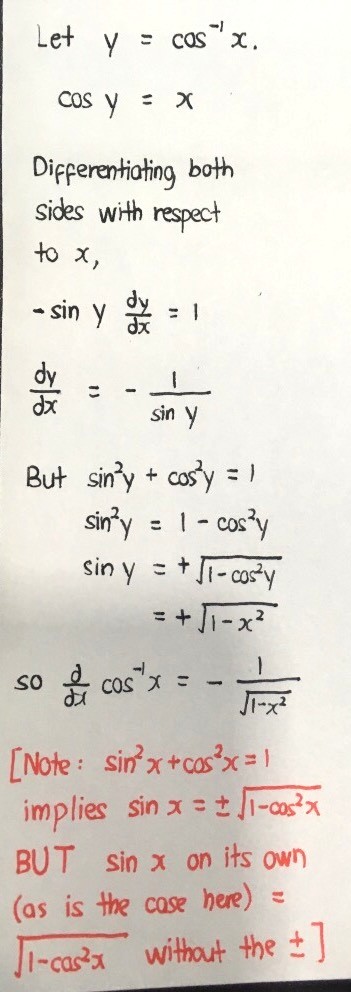
when -1 < x < 1, 0 < cos-1(x) < π

sin y = sin(cos-1(x))

Since 0 < cos-1(x) < π,

0 < siny < 1

So sin y is always positive for this range. No ± is needed

Update: if you would like to know why it's restricted, you can check out this link :

https://www.themathpage.com/atrig/inverseTrig.htm#abs

Eric Nicholas K

5 years ago

Hmmm...I did think of the [0, pi] limit but completely forgot that sin of the number between those is never negative

5 years ago

Actually back in JC the explanations for these were never covered... picked it up over the years