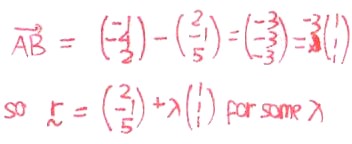Eric Nicholas K's answer to beebop's Junior College 1 H2 Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
We find the direction vector AB, which is simply the 'difference' between the positions A and B. The order does not matter; we are only interested in the 'gradient' (just like a two-dimensional straight line y = mx + c).
We extract out 1 1 1 from -3 -3 -3 (or 3 3 3 if you had done A - B). This is the direction vector for AB.
Of course, for two parallel lines, they have the same direction vector (akin to 'gradient'). Since the line passes A or B, your equation becomes
r = (either point A or B) + k (1 1 1) for some real k.
We extract out 1 1 1 from -3 -3 -3 (or 3 3 3 if you had done A - B). This is the direction vector for AB.
Of course, for two parallel lines, they have the same direction vector (akin to 'gradient'). Since the line passes A or B, your equation becomes
r = (either point A or B) + k (1 1 1) for some real k.
Date Posted:
5 years ago
360 Tutoring Program