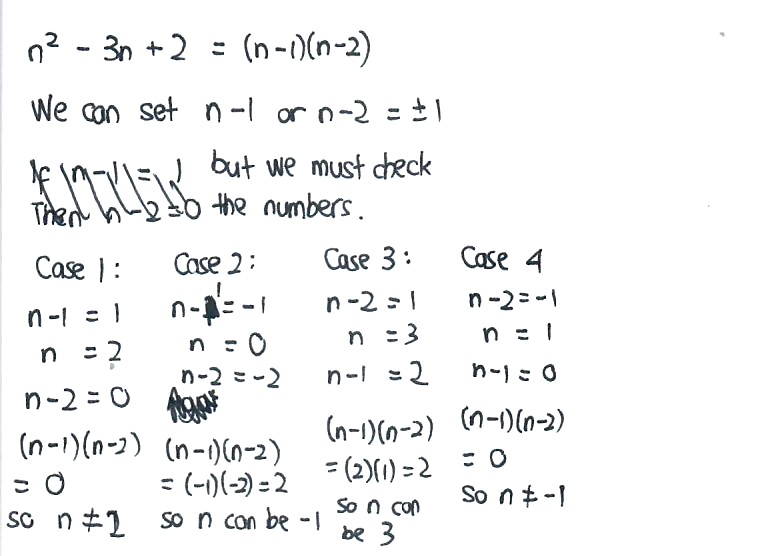Eric Nicholas K's answer to Kathy's Secondary 4 A Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
The first question goes like this. I will explain the concept more clearly here in this text.
First, we factorise the expression using cross-factorisation.
Factorising the expression yields (n - 1) (n - 2).
Now, (n - 1) represents a number; so does (n - 2), so (n - 1) (n - 2) is just simply the product of two numbers. For example, if n = 5, then (n - 1) equals 4 and (n - 2) equals 3, so (n - 1) (n - 2) is the product of 4 and 3.
A prime number is a positive integer which can be divided by 1 and itself (the definition does not include 0 and 1 as a prime number).
For the product (n - 1) (n - 2) to be a prime number, either of the bracketed numbers must equal to 1 (or -1 in some cases). It's alright for one of the numbers in the bracket to be -1, so long as the other number also has a negative sign (so that the product of two negative numbers is a positive number). However, obtaining 1 or -1 does not automatically mean that multiplication with the other number yields a prime number, so we must check accordingly.
There are four cases to consider by setting (n - 1) = 1, (n - 1) = -1, (n - 2) = 1 and (n - 2) = -1.
CASE 1 -----> (n - 1) = 1
Setting (n - 1) = 1, we get n = 2. This gets us (n - 2) = 0, and (n - 1) (n - 2) = 1 x 0 = 0 is not a prime number. So, n cannot be 2, and this case is rejected.
CASE 2 -----> (n - 1) = -1
Setting (n - 1) = -1, we get n = 0. This gets us (n - 2) = -2, and (n - 1) (n - 2) = (-1) x (-2) = 2 is a prime number. So, n can be 0.
CASE 3 -----> (n - 2) = 1
Setting (n - 2) = 1, we get n = 3. This gets us (n - 1) = 2, and (n - 1) (n - 2) = 2 x 1 = 2 is a prime number. So, n can be 3.
CASE 4 -----> (n - 2) = -1
Setting (n - 2) = -1, we get n = 1. This gets us (n - 1) = 0, and (n - 1) (n - 2) = 0 x (-1) = 0 is not a prime number. So, n cannot be 1, and this case is rejected.
All other values of n will not get you a prime number. For example, if n = 5, then (n - 1) (n - 2) = 4 x 3 which obviously does not equate to a prime number (which is the basis of why we must set either of the bracketed terms to 1 or -1).
Hence, n can be 0 or 3.
First, we factorise the expression using cross-factorisation.
Factorising the expression yields (n - 1) (n - 2).
Now, (n - 1) represents a number; so does (n - 2), so (n - 1) (n - 2) is just simply the product of two numbers. For example, if n = 5, then (n - 1) equals 4 and (n - 2) equals 3, so (n - 1) (n - 2) is the product of 4 and 3.
A prime number is a positive integer which can be divided by 1 and itself (the definition does not include 0 and 1 as a prime number).
For the product (n - 1) (n - 2) to be a prime number, either of the bracketed numbers must equal to 1 (or -1 in some cases). It's alright for one of the numbers in the bracket to be -1, so long as the other number also has a negative sign (so that the product of two negative numbers is a positive number). However, obtaining 1 or -1 does not automatically mean that multiplication with the other number yields a prime number, so we must check accordingly.
There are four cases to consider by setting (n - 1) = 1, (n - 1) = -1, (n - 2) = 1 and (n - 2) = -1.
CASE 1 -----> (n - 1) = 1
Setting (n - 1) = 1, we get n = 2. This gets us (n - 2) = 0, and (n - 1) (n - 2) = 1 x 0 = 0 is not a prime number. So, n cannot be 2, and this case is rejected.
CASE 2 -----> (n - 1) = -1
Setting (n - 1) = -1, we get n = 0. This gets us (n - 2) = -2, and (n - 1) (n - 2) = (-1) x (-2) = 2 is a prime number. So, n can be 0.
CASE 3 -----> (n - 2) = 1
Setting (n - 2) = 1, we get n = 3. This gets us (n - 1) = 2, and (n - 1) (n - 2) = 2 x 1 = 2 is a prime number. So, n can be 3.
CASE 4 -----> (n - 2) = -1
Setting (n - 2) = -1, we get n = 1. This gets us (n - 1) = 0, and (n - 1) (n - 2) = 0 x (-1) = 0 is not a prime number. So, n cannot be 1, and this case is rejected.
All other values of n will not get you a prime number. For example, if n = 5, then (n - 1) (n - 2) = 4 x 3 which obviously does not equate to a prime number (which is the basis of why we must set either of the bracketed terms to 1 or -1).
Hence, n can be 0 or 3.
Date Posted:
5 years ago
Correction to my case 2 on the scanned document: n = 0.