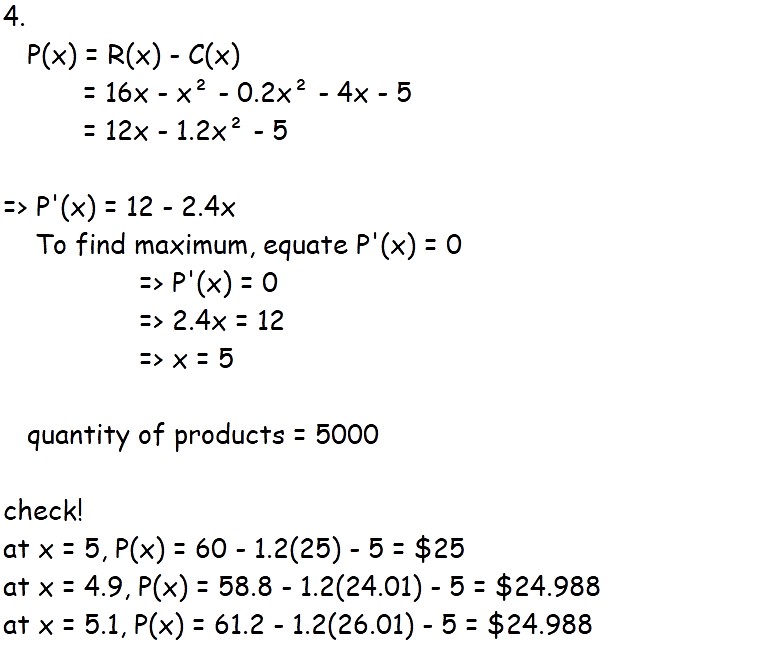How did px suddenly became this (12-2.4x)

it is not P(x),
it is P'(x), a derivative of P(x).
meaning
differentiate P(x) wrt x

Ok thanks for your help! Though we do not learn differentiation in sec 4

oh, u dun take AMath?

then to find the max. u hv to follow a tedious method of completing the square to find the max point.

complete the square:
P(x) = -1.2x² + 12x - 5
= -1.2(x²-10x) - 5
= -1.2(x²-10x+25) - 5 +30
= -1.2(x-5)² + 25

this means max pt is at (5, 25).

how?
bcos of (x-5)², we know the x-coordinates of max pt is 5.
[equate x-5=0 => x=5]

then subst. x=5 into P(x):
P(x) = -1.2(5-5)² + 25
= 0 + 25 = 25

max profit P(x) = 25.

and

u r welcome!

This is what im looking for thank you so much

So the ans would be 25000?

nope. sorry.

the qn asks for quantity of products, i.e. x ;
we found x = 5 ;

so the ans is 5000, bcos the qn states x is in thousands.

leaving this thread now.
any more qns, send to: [email protected]