Ivan Chew's answer to nsn's Junior College 1 H3 Maths question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
The question would be simpler if the cheetah is jumping VERTICALLY. However, since the cheetah is jumping diagonally, find the vertical component first (since you don't care how much the cheetah moves horizontally)
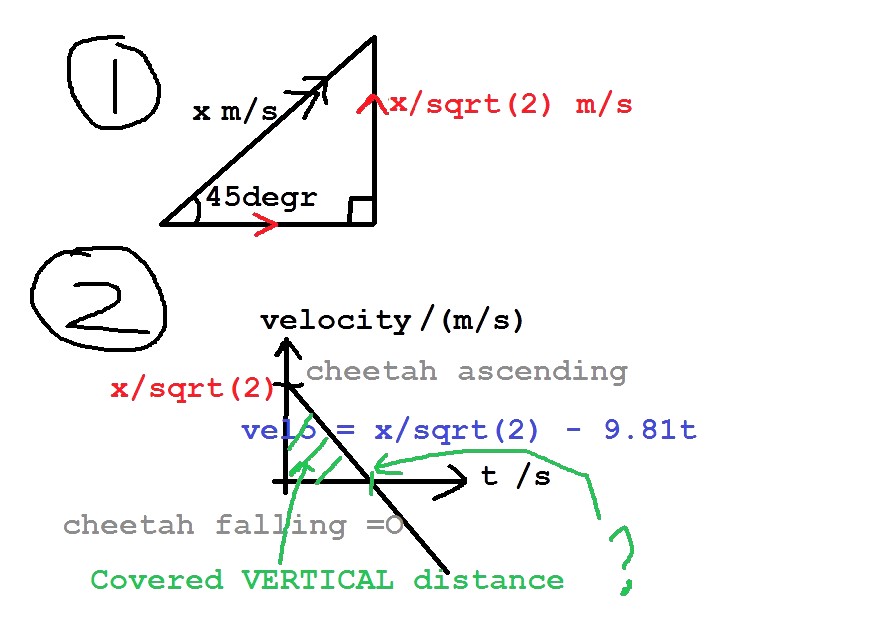
1)
Let the initial diagonal speed = x m/s
Initial VERTICAL speed
= x sin(45degr) m/s
= x/sqrt(2) m/s
2)
Assume deceleration due to gravity is 9.81 m/s^2
Cheetah reaches max height at time
x/sqrt(2) m/s / 9.81 m/s^2
= x/9.81sqrt(2) s
Max height = Area under the triangle
3.7m = 1/2 * time taken to reach max ht * initial VERTICAL speed
3.7 = 1/2 * x * x / sqrt(2) / 9.81sqrt(2)
3.7 = x^2 / 9.81 / 4
x^2 = 145.188
x = 12.0 (x > 0 as cheetah is airborne not underground =X )
1)
Let the initial diagonal speed = x m/s
Initial VERTICAL speed
= x sin(45degr) m/s
= x/sqrt(2) m/s
2)
Assume deceleration due to gravity is 9.81 m/s^2
Cheetah reaches max height at time
x/sqrt(2) m/s / 9.81 m/s^2
= x/9.81sqrt(2) s
Max height = Area under the triangle
3.7m = 1/2 * time taken to reach max ht * initial VERTICAL speed
3.7 = 1/2 * x * x / sqrt(2) / 9.81sqrt(2)
3.7 = x^2 / 9.81 / 4
x^2 = 145.188
x = 12.0 (x > 0 as cheetah is airborne not underground =X )
Date Posted:
6 years ago
360 Tutoring Program