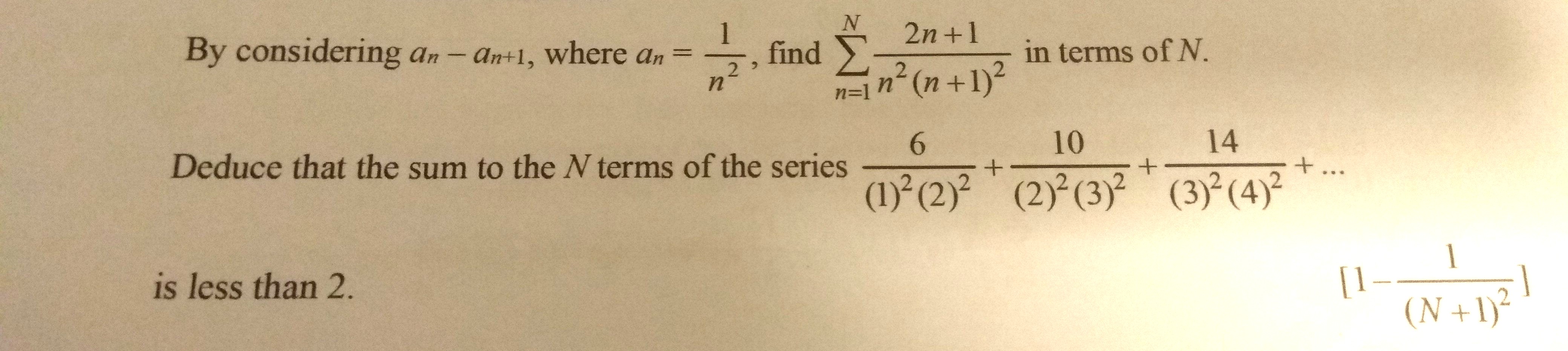snell's answer to Rowan's Junior College 1 H2 Maths question.
done
1 Upvotes
clear 0 Downvotes

aₙ = 1/n²
aₙ - aₙ₊₁ = 1/n² - 1/(n+1)²
= [(n+1)² - n²]/[n²(n+1)²]
= (2n + 1)/[n²(n+1)²]
Σ(2n + 1)/[n²(n+1)²]|1 to N
= Σ[1/n² - 1/(n+1)²]|1 to N
= 1/1² - 1/2² ... (n=1)
+ 1/2² - 1/3² ... (n=2)
+ 1/3² - 1/4² ... (n=3)
+ 1/4² - 1/5² ... (n=4)
+ 1/5² - 1/6² ... (n=5)
.
.
.
.
+ 1/(N-3)² - 1/(N-2)² ... (n=N-3)
+ 1/(N-2)² - 1/(N-1)² ... (n=N-2)
+ 1/(N-1)² - 1/(N)² ... (n=N-1)
+ 1/N² - 1/(N+1)² ... (n=N)
= 1 - 1/(N+1)²
(6)/(1)²(2)² + (10)/(2)²(3)² + (14)/(3)²(4)² + ... to N terms
= 2[2(1) + 1]/(1)²(1+1)² + 2[2(2) + 1]/[(2)²(2+1)²]
+ 2[2(3) + 1]/[(3)²(3+1)²] + ... to N terms
= 2[1 - 1/(N+1)²]
For all values of N, 1/(N+1)² is less than 1,
=> [1 - 1/(N+1)²] is also less than 1,
hence, 2[1 - 1/(N+1)²] is less than 2
aₙ - aₙ₊₁ = 1/n² - 1/(n+1)²
= [(n+1)² - n²]/[n²(n+1)²]
= (2n + 1)/[n²(n+1)²]
Σ(2n + 1)/[n²(n+1)²]|1 to N
= Σ[1/n² - 1/(n+1)²]|1 to N
= 1/1² - 1/2² ... (n=1)
+ 1/2² - 1/3² ... (n=2)
+ 1/3² - 1/4² ... (n=3)
+ 1/4² - 1/5² ... (n=4)
+ 1/5² - 1/6² ... (n=5)
.
.
.
.
+ 1/(N-3)² - 1/(N-2)² ... (n=N-3)
+ 1/(N-2)² - 1/(N-1)² ... (n=N-2)
+ 1/(N-1)² - 1/(N)² ... (n=N-1)
+ 1/N² - 1/(N+1)² ... (n=N)
= 1 - 1/(N+1)²
(6)/(1)²(2)² + (10)/(2)²(3)² + (14)/(3)²(4)² + ... to N terms
= 2[2(1) + 1]/(1)²(1+1)² + 2[2(2) + 1]/[(2)²(2+1)²]
+ 2[2(3) + 1]/[(3)²(3+1)²] + ... to N terms
= 2[1 - 1/(N+1)²]
For all values of N, 1/(N+1)² is less than 1,
=> [1 - 1/(N+1)²] is also less than 1,
hence, 2[1 - 1/(N+1)²] is less than 2
Date Posted:
6 years ago