Let area of ∆ DEF be 1 unit.

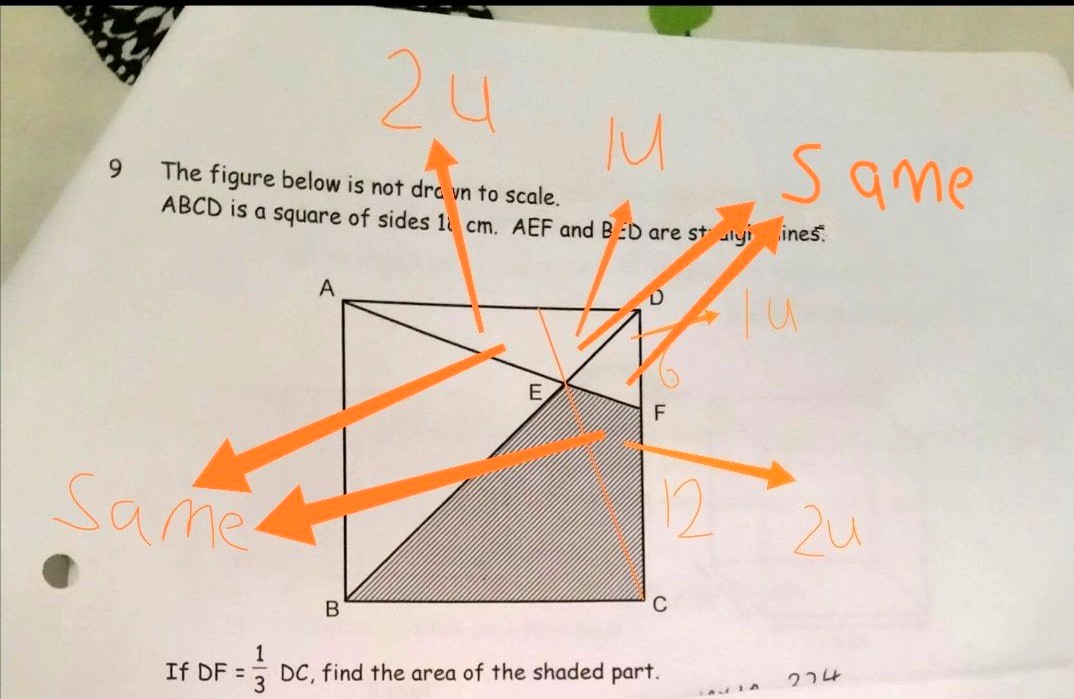
∆CEF's base is twice that of ∆DEF,
and they have same height,

Area of ∆CEF = 2 units.

You can see from the diagram that the triangles on the other side are the same.

Area of ∆ ADF = 2 units + 1 unit + 1 unit
= 4 units

Area of ∆ ADF = 1/2 x base x height
= 1/2 x 6 x 18 = 54 cm²

So 4 units = 54 cm²

1 unit = 54 cm² ÷ 4 = 13.5 cm²

Area of shaded part

= Area of ∆ DBC - Area of ∆ DEF
= 1/2 x 18 x 18 - 1 unit
= 162 cm² - 13.5 cm²

= 148.5 cm²