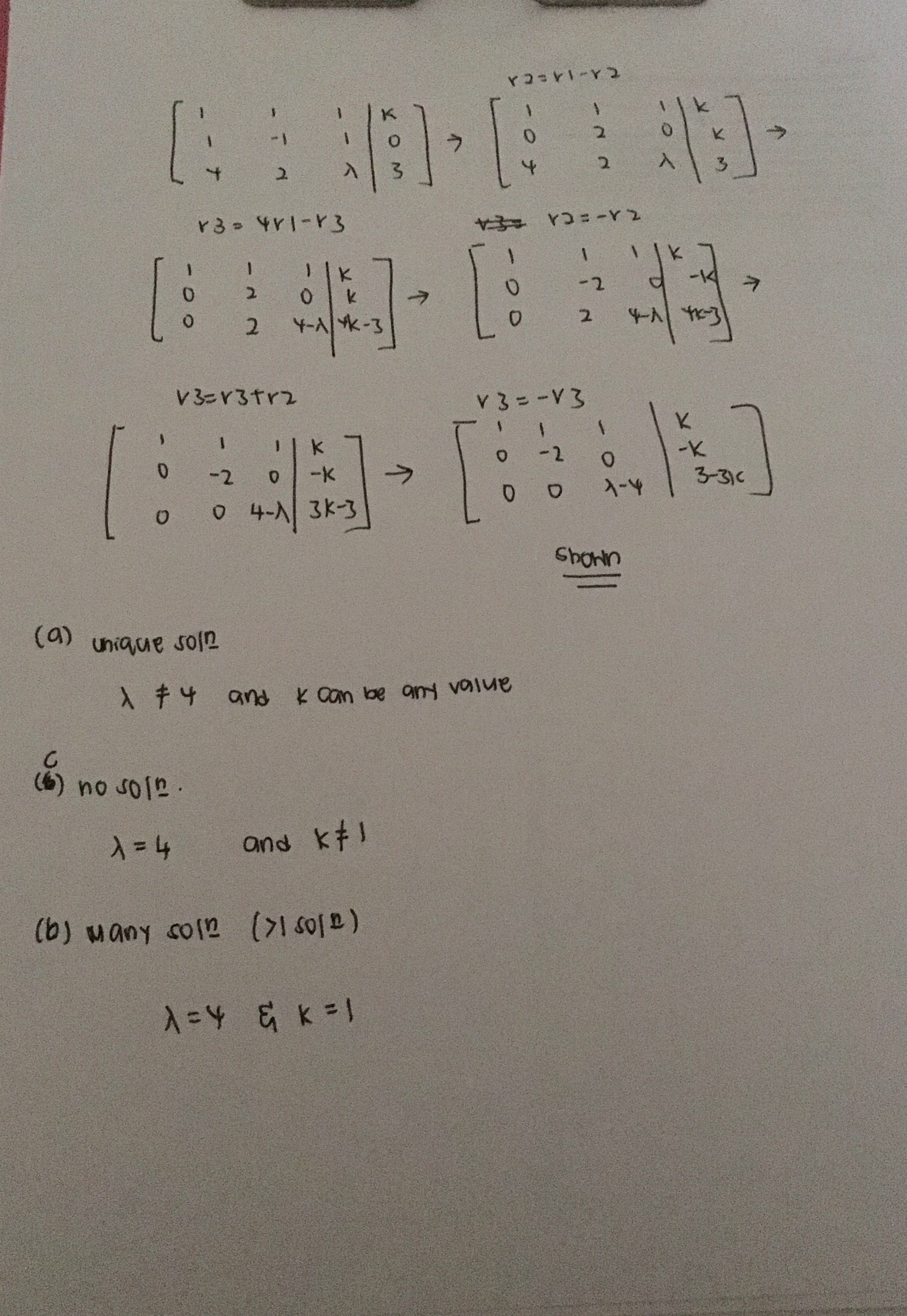Low Shu En's answer to Newzealand's Junior College 1 H1 Maths question.
Since x is the leading variable of the row 1. Y is the leading variable of row 2 and z is the leading variable of row 3. Which means you are going to write the eqn of each row in terms of these leading variables.
Since row 3 is the one that involves landa, hence i only look at row 3.
Unique solution means that x, y and z will have a value respectively. For z to have a value (landa - 4) should not be equals to 0. Else the last eqn would be 0z = 3-3k. Hence in order for it not to be 0z, landa must not be equals to 4.
For k, it can be any value as it does not matter what value z takes. As long as it takes on a value. Meaning 0 is also acceptable.
Since row 3 is the one that involves landa, hence i only look at row 3.
Unique solution means that x, y and z will have a value respectively. For z to have a value (landa - 4) should not be equals to 0. Else the last eqn would be 0z = 3-3k. Hence in order for it not to be 0z, landa must not be equals to 4.
For k, it can be any value as it does not matter what value z takes. As long as it takes on a value. Meaning 0 is also acceptable.
For part b. In order to have many solutions it means to say that z will be taking an arbitary constant. Meaning z can hold on to any value as z is unknown to us.
In this case, the idea is to make z unknown. This means landa-4 should be 0 and 3-3k should also be 0. Means to say that landa=4 and k=1
In this case, the idea is to make z unknown. This means landa-4 should be 0 and 3-3k should also be 0. Means to say that landa=4 and k=1
For part c. I would usually think of no solution as having an eqn that does not make sense.
E.g.: 0z = some value but not 0
Hence to make 0z, landa-4 = 0, means landa = 4.
To make right hand side not equals to 0, It only means that k is not equals to 1.
E.g.: 0z = some value but not 0
Hence to make 0z, landa-4 = 0, means landa = 4.
To make right hand side not equals to 0, It only means that k is not equals to 1.