ohh i understand now, thank you. btw is it possible for tan 5x = tan 2x to be tan5x - tan 2x and just get tan 3x as my equation. and find alpha, which = 0, and since 0 is on the same line as 180° which is also where the tangent quad is at. so can i just take 180, 180×2, 180×3 and so on and ÷ all the answers by 3 since its 3x?? is this an appropriate way of doing it too??

Firstly tan5x -tan2x is not equal to tan3x. Secondly, alpha (basic/reference angle) cannot be zero or 90 degrees. This is because if alpha is zero, you cannot deduce which quadrant the the angle lies on. So when you solve questions like sinx/cosx = 0/1/-1, you shld draw a graph to determine the values of x

ahh, ok i get it, thank you so much !!

Alternative approach is to do this:

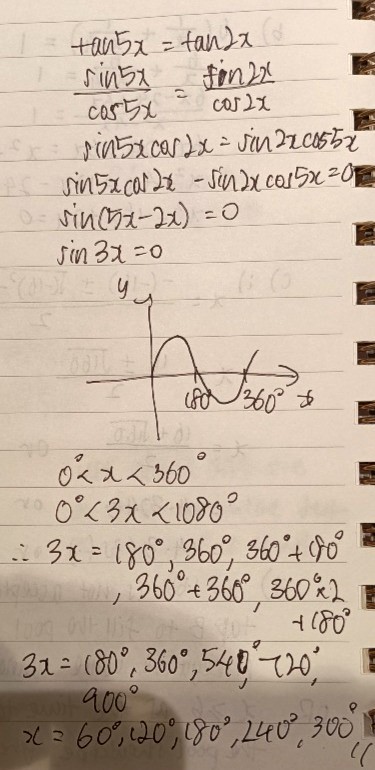
tan 5x = tan 2x
tan 5x - tan 2x = 0

Then we divide both sides by (1 + tan 5x tan 2x). Since tan 5x = tan 2x, the value of tan 5x tan 2x will be at least zero, so we won’t run into zero denominator issues.

The left-hand side will look very much like the tangent addition formula!

tan (5x - 2x) = 0
tan 3x = 0

And you can follow the tutor’s workings afterwards.

The operation for trigonometric functions is not quite like regular algebraic expressions.

Sine, cosine and tangent are actually length ratio operators in triangles and should not be treated as algebraic.

In particular, we cannot, for example, say that sin (A + B) = sin A + sin B, in contrast with expressions such as k (A + B) = kA + kB.

When you learnt sine, for example, it was defined as the trigonometric ratio of the length of an opposite side to the hypotenuse side of a triangle with respect to a particular angle chosen.

Most people would have forgotten about this “ratio” word in trigonometry and some people would then accordingly make the error of “expanding” or “factorising” such expressions.

Logarithmic expressions are also similar; they are another type of operator altogether and in a similar way, log (A + B) is not equivalent to log A + log B in general.