Boy Mow Chau's answer to Astrid's Junior College 1 H2 Maths Singapore question.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
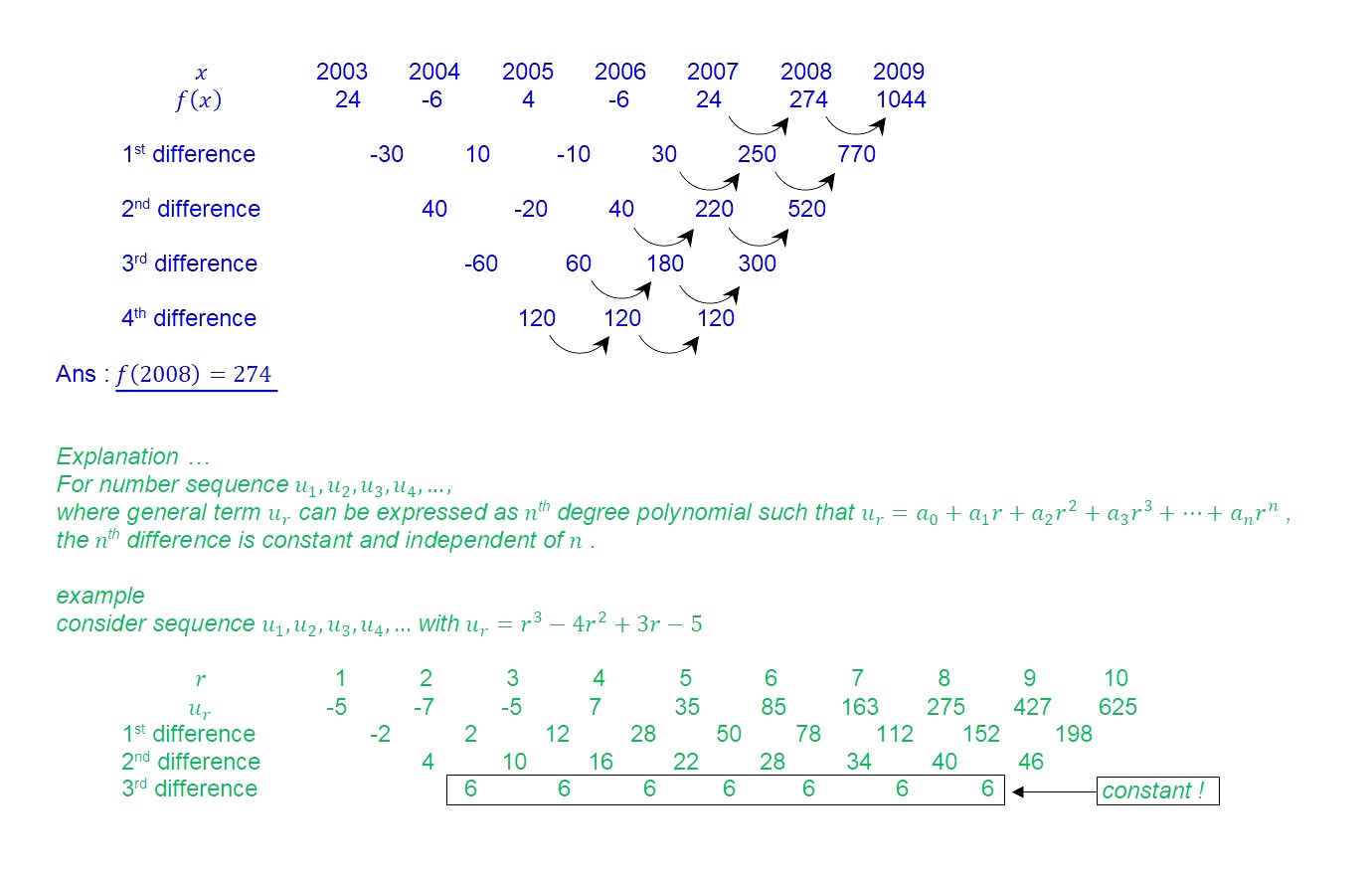
normally for such questions, can just substitute the appropriate values into the polynomial function to form a system of linear equations, and solve using GC, to obtain the coefficients. however, the numbers here are beyond what the GC is able to crunch (2003^4 is 14 digits long!).
the problem can be solved through an understanding of the behavior of number sequences (refer to explanation below the solution).
this question is unlikely to be within H2 Maths syllabus, and also not in H2 Further Maths syllabus. can you please enlighten us what course/level this question is from?
the problem can be solved through an understanding of the behavior of number sequences (refer to explanation below the solution).
this question is unlikely to be within H2 Maths syllabus, and also not in H2 Further Maths syllabus. can you please enlighten us what course/level this question is from?
Date Posted:
2 years ago
by the way, recall remainder theorem from O level A Maths ....
when divided by (x-2003), f(x) has remainder 24 means f(2003) = 24, and so on.
the values 2003, 2004, etc, do not affect the value of the 4th difference. for polynomial of degree nth, the nth difference is constant and equals ...
n! x coef. of x^n term.
when divided by (x-2003), f(x) has remainder 24 means f(2003) = 24, and so on.
the values 2003, 2004, etc, do not affect the value of the 4th difference. for polynomial of degree nth, the nth difference is constant and equals ...
n! x coef. of x^n term.