Eric Nicholas K's answer to Nelson Loo's Junior College 2 H2 Maths Singapore question.
done
1 Upvotes
clear 0 Downvotes
Like this perhaps? Seems like it need not be split after all
Date Posted:
3 years ago
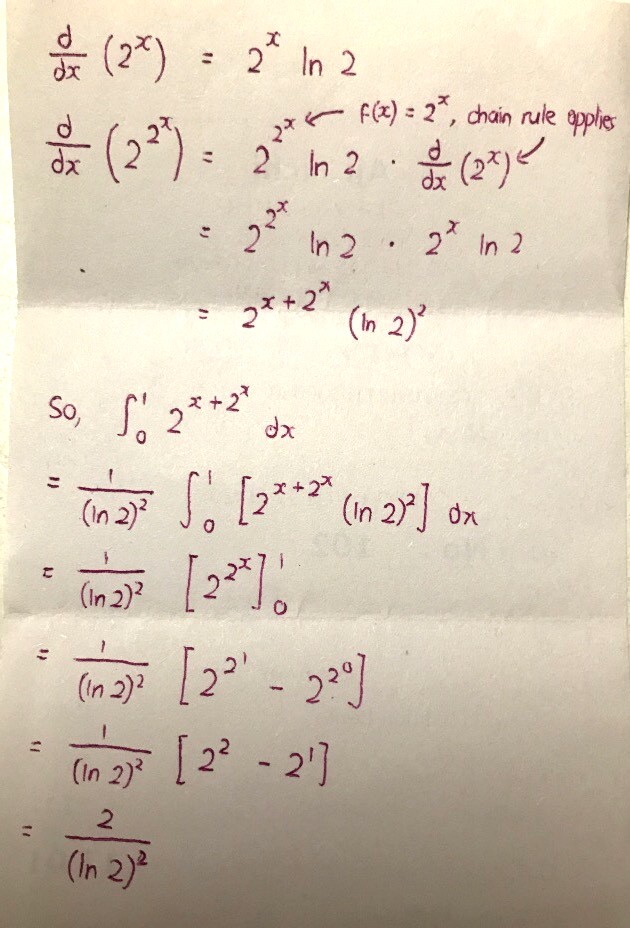


Recall that : d/dx aᶠ⁽ˣ⁾ = f'(x) · aᶠ⁽ˣ⁾ · ln a
So, you can just split the indices like this.
∫¹₀ 2ˣ⁺²^ˣ dx
= ∫¹₀ 2ˣ · 2²^ˣ dx
Then, introduce back in a ln2 for each of the terms.
= (1/ln2)² ∫¹₀ 2ˣ ln2 · 2²^ˣ ln2 dx
Whereby your a = 2, f(x) = 2ˣ and f'(x) = 2ˣ ln2
= 1/(ln2)² [2²^ˣ]∫¹₀
= 1/(ln2)² (2²^¹ - 2²^⁰)
= 2/(ln2)²
(Since 2²^¹ - 2²^⁰ = 2² - 2¹ = 4 - 2 = 2)
The question tests your ability to visualise/realise that it is directly integrable and can be rewritten.