learn to say more thanks

Q7ii

There are two components to the cost of goods produced (though this is higher level stuff).

One of them is called the fixed costs. This cost will remain fixed regardless of the performance of the sales. For example, rental costs and equipment costs are a good example of fixed costs as these are agreed on by the respective owners and buyers.

The other is called the variable costs which depend on the number of goods sold or produced. This is where the sales volume of goods kicks in.

Imagine purchasing an equipment and renting floor space for a total of $5000 just to...produce one carton of a juice. It does not make sense, correct?

Using the same machine and space, we can produce thousands or even millions of cartons of juice. This taps on what we call the economies of scale such that the fixed costs will be distributed equally among the number of goods sold.

Q9

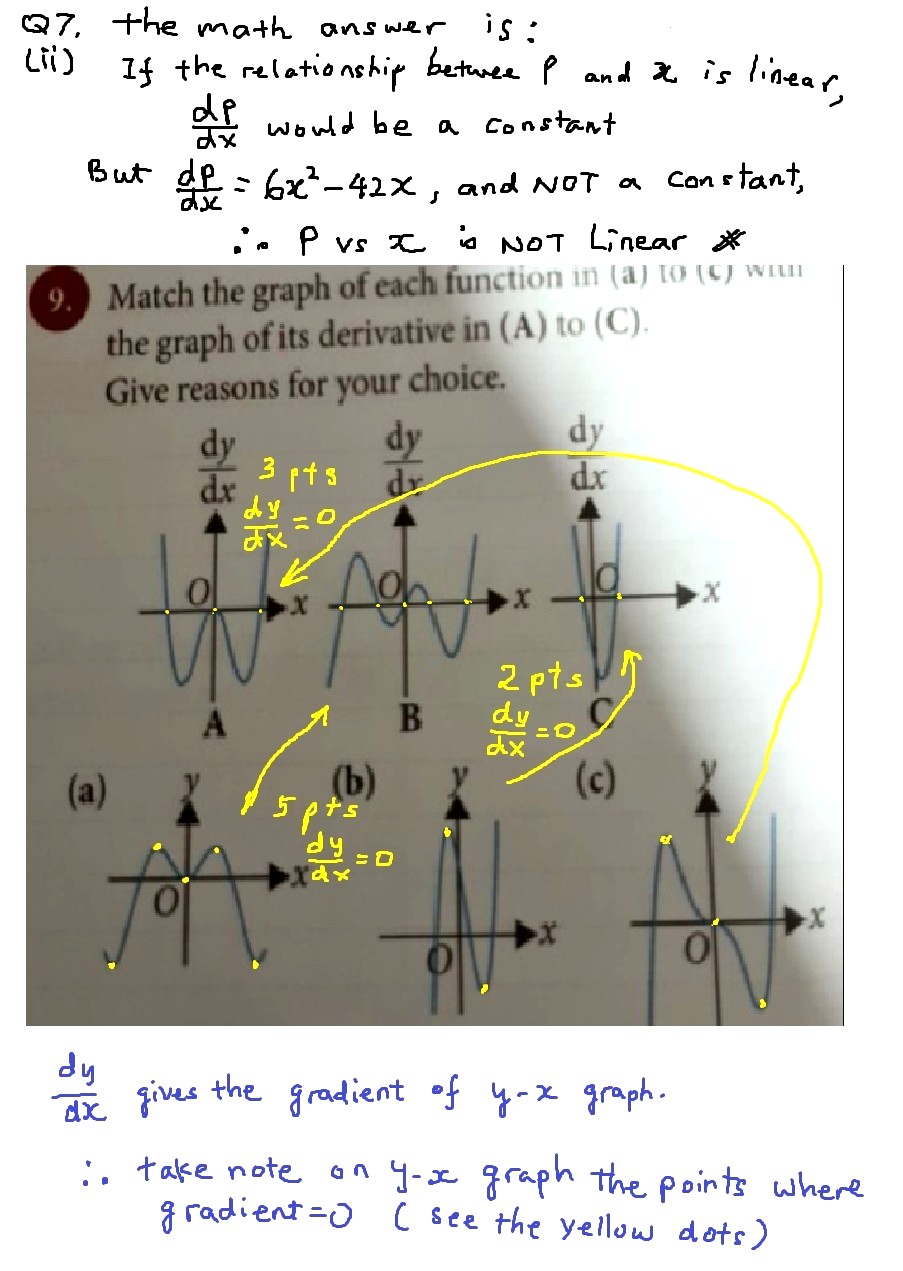
(a) corresponds to B. Since the graph in (a) has five turning points, there will be five points at which dy/dx = 0. On the graph labelled dy/dx, "dy/dx = 0" is represented by intercepts of the x-axis, so there are five x-intercepts in total in the graph of dy/dx against x. There are other characteristics including the signage of dy/dx to consider and the graph in B fits the graph in (a) well.

(b) corresponds to C due to the existence of two turning points.

(c) corresponds to A due to the existence of three turning points.

This question requires you to have a thorough understanding of the first derivatives of the function and their corresponding first derivative test.

for qn 9,turning point is the curved part or....? i only saw a turning point at C and the others doesnt match
dont really understand why is the point on x-axis considered and not the curved part...

"for qn 9,turning point is the curved part or....? i only saw a turning point at C and the others doesnt match

dont really understand why is the point on x-axis considered and not the curved part..."

-------------------------------------------------------

You need to understand how linear law (or similar idea) works first before understanding this part. In other words, you must be able to accept the fact that the vertical axis is not always called "y".

Remember that at the turning points of the original graph, dy/dx = 0. At these points, the graphs appear to come to a horizontal halt, regardless of whether the stationary point is a minimum, maximum or inflection.

So in the graph of dy/dx against x, these turning points on the original curve would appear as an x-intercept on this graph, because dy/dx = 0 at these points.

Let's say we have a graph of y = x² - 2x - 3.

dy/dx = 2x - 2

At the stationary point,
dy/dx = 0
2x - 2 = 0
x = 1
y = 1² - 2 (1) - 3 = -4

So, the stationary point is (1, -4). This will be a minimum point on the original graph.

On the graph of dy/dx, we only plot values of dy/dx against x. We now know that when x = 1, dy/dx = 0.

This will appear as the coordinate (1, 0) on the graph of dy/dx against x. This corresponds to the minimum point (1, -4) on the main graph.

But we very well know that (1, 0) is a point on the x-axis. So, in the graph of dy/dx against x, this stationary point of the original curve (1, -4), which is reflected as (1, 0) on this gradient curve, will be an x-intercept on the graph.

This is why all stationary points on the original graph will translate to x-intercepts on the gradient graph.

As an added bonus for you to know, the regions on the gradient graph which lie above to the x-axis (i.e. positive region) correspond to the regions on the original graph which are increasing (you should have learnt increasing and decreasing functions by now), and a similar argument applies to regions below the x-axis on the gradient graph.