Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
Secondary 1 | Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

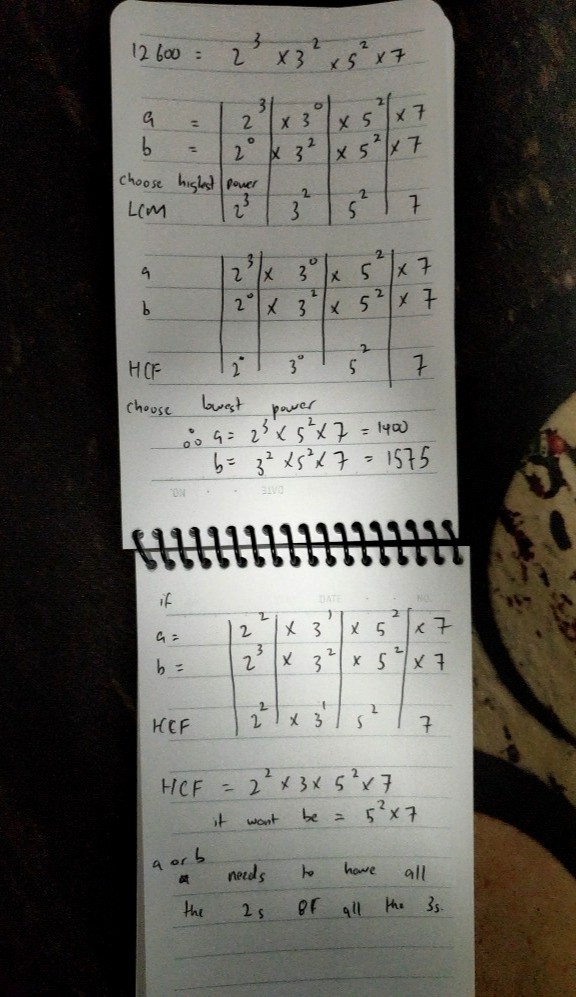
Question involving HCF and LCM.
I've worked out this so far but I'm not sure what to do next? I looked at the textbook's example but it's just confusing. If you could, please explain your answer. Thank you for the help. :)
So all their common factors consist of 5² and 7 only.
Each number also has some other factors that the other doesn't have.
Now, the LCM has a 2³ and a 3².
Since they have no other common factors other than 5² and 7, then this means 1 number has 2³ and not 3², and likewise, the other number has 3² and not 2³.
This is why the LCM has to have both 3² and 2³ such that it is the smallest possible number that can be divided by both numbers exactly.
(If they had least one 3 or 2 each, then 2 and 3 are also common factors , which means the HCF would be higher than 175 already)
So the numbers are :
175 x 2³ = 175 x 8 = 1400
And
175 x 3² = 175 x 9 = 1575
and the LCM as a set of all the prime factors from both numbers, but without double counting the overlap.
Eg.
36 = 2 x 3 x 3 x 2 = 2² x 3²
150 = 5 x 5 x 3 x 2 = 5² x 3 x 2
Both numbers have one 2 and one 3 in common ('overlapping').
HCF = 3 x 2 = 6
A set of prime factors that covers both numbers without double counting the overlap would be :
[2,3,(3,2],5,5)
The square brackets cover all the prime factors of 36 and the curved brackets cover all the prime factors of 150.
In between, we can see that they have one 2 and 3 common. This is the overlap (HCF)
The LCM would be the entire set , but not double counting the overlap.
LCM = 2 x 2 x 3 x 3 x 5 x 5
= 2² x 3² x 5²
= 4 x 9 x 25
= 900
The HCF is akin to the overlapping area, and the LCM is akin to the total area of the figure.
Another thing to remember :
HCF x LCM = product of both numbers.
If we list out all the prime factors and take out the LCM, we are left with the HCF.
This is like the area of figure , whereby combined area of both shapes = area of figure + area of overlap
Didn't know about that one :)
See 2 Answers