Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

See 2 Answers
Recall the algebraic identity (a + b)² = a² + 2ab + b².
So what we need to do is to rewrite ¼ + x + x² into this form.
¼ + x + x²
= (½)² + 2(½)(x) + x²
= (½ + x)²
Here, our a = ½ and b = x
Alternatively, since a and b are actually interchangeable since a + b = b + a.
So we could rewrite it as (x + ½)²
= x² + 2(x)(½) + (½)²
= x² + x + ¼
Here, our a = x and b = ½
So what we need to do is to rewrite ¼ + x + x² into this form.
¼ + x + x²
= (½)² + 2(½)(x) + x²
= (½ + x)²
Here, our a = ½ and b = x
Alternatively, since a and b are actually interchangeable since a + b = b + a.
So we could rewrite it as (x + ½)²
= x² + 2(x)(½) + (½)²
= x² + x + ¼
Here, our a = x and b = ½
Cross factorisation is more appealing to me.
Or, I could factor out a 1/4 to make it easier to the eye.
1/4 + x + x^2
= 1/4 (1 + 4x + 4x^2)
= ...
And then we split 1/4 as 1/2 x 1/2 before integrating them into each bracket.
Or, I could factor out a 1/4 to make it easier to the eye.
1/4 + x + x^2
= 1/4 (1 + 4x + 4x^2)
= ...
And then we split 1/4 as 1/2 x 1/2 before integrating them into each bracket.
Perhaps an assured method, but slow and troublesome.
Students should build intuition in knowing how to spot factors out from expressions.
This example is fairly simple anyway.
Students should build intuition in knowing how to spot factors out from expressions.
This example is fairly simple anyway.
Anyway, the student asked to factorise by algebraic identities so rewriting in the a² + 2ab + b² form is probably what she wants, rather than cross factorisation.
The most probable reason why the student brought up the question is that he/she is unable to spot the factorisation together when one or more of the values are in fraction form.
That's the whole point of this question. Learning to spot factors.
Things like 1/9 = (⅓)² , ¼ = (½)² , x = ½(2)x and ¼x = 2(⅛)x = 2(½)(¼x) = 2(¼)(½x)
At higher levels, these would become second nature
Things like 1/9 = (⅓)² , ¼ = (½)² , x = ½(2)x and ¼x = 2(⅛)x = 2(½)(¼x) = 2(¼)(½x)
At higher levels, these would become second nature



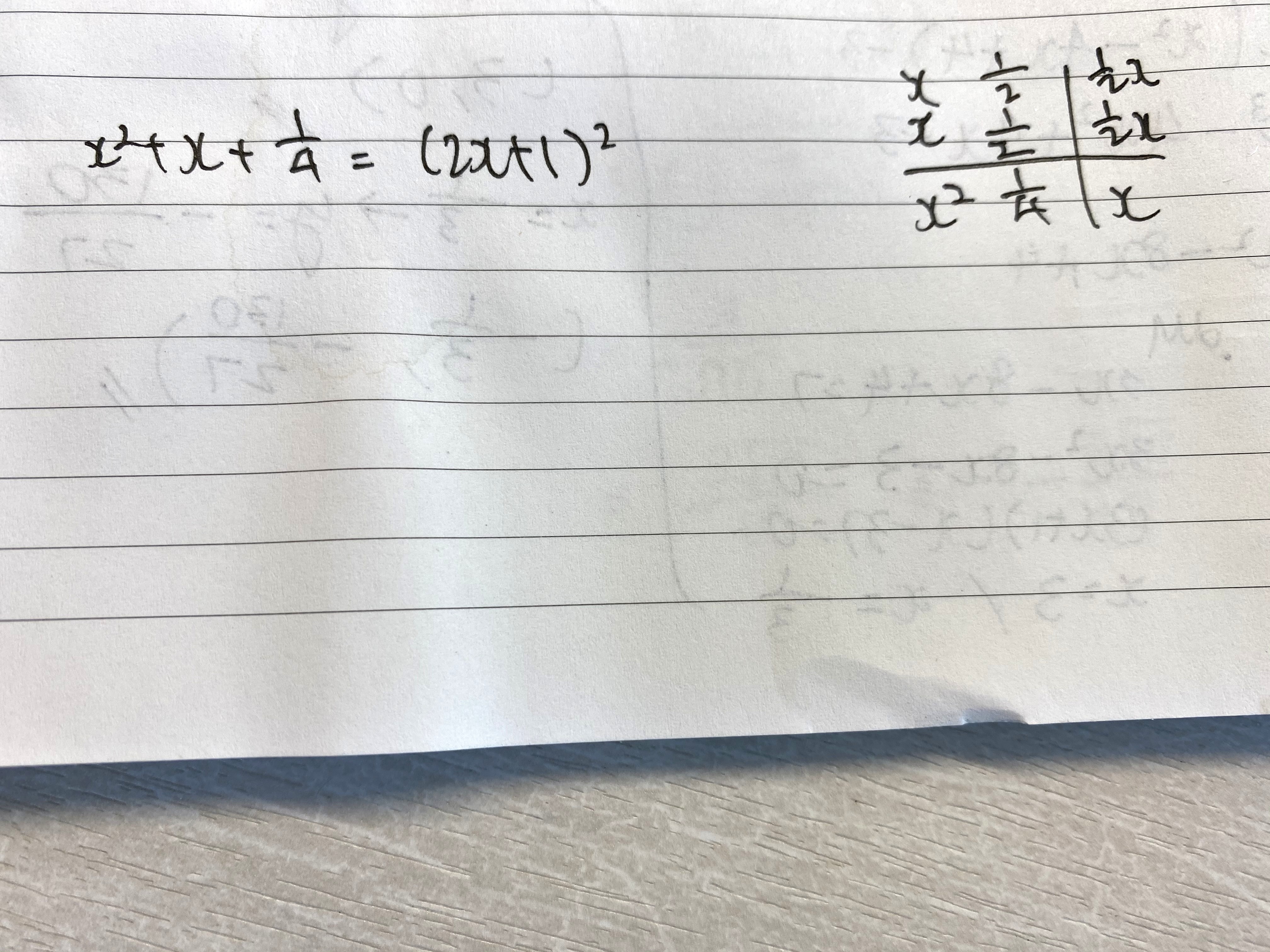




It’s (x + 0.5)^2.
You must not convert the (x + 0.5) into (2x + 1) because this is not an equation. This is an expression.