Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 2 | H2 Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

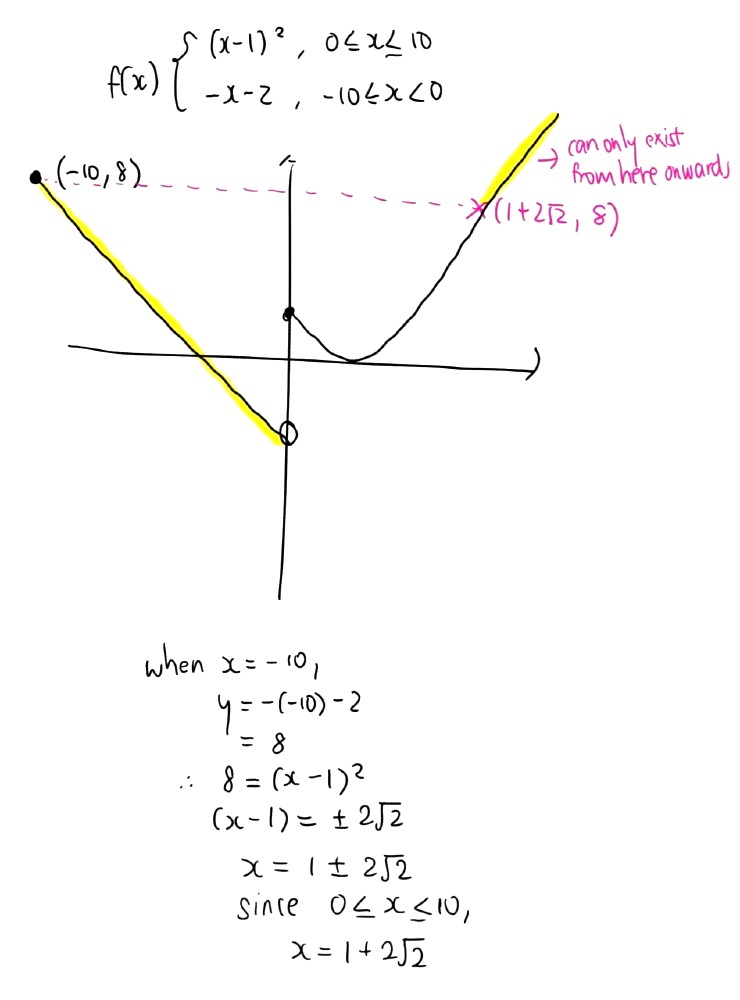
Just part (ii) will suffice. Does anyone know why the answer given is [-10, 0) U [1+2√2, 10) and not [-10, 0) U [2, 10). Isn't the function already 1-1 and therefore f inverse exists from x=2 onwards? So [2, 10) would be the largest domain here.
To have an inverse, the function's domain has to be restricted such that it is 1-to-1 .
1-to-1 means that every input value corresponds to exactly 1 unique output value only.
We cannot have 2 input values giving the same output value. (i.e can't have 2 x-values giving the same f(x) value)
Now,
For -10 ≤ x < 0, 8 ≤ f(x) < -2
For 0 ≤ x ≤ 10, 0 ≤ f(x) ≤ 81
What we know about the (x-1)² portion on the right side of the x-axis is that:
The f(x) value first decreases from 1 at x = 0 to 0 at x = 1.
It then increases from 0 to 81 when x increases from 1 to x = 10
But on the left portion of the x-axis, f(x) is also increasing. It is increasing linearly to 8 at x = -10
So we would have two or even three different x-values giving the same f(x) value. This is definitely not 1-to-1.
We cannot restrict the (x - 1)² part to 1 ≤ x ≤ 10 only , because that only makes this part 1-to-1. The whole function is not 1-to-1 yet.
Some values of x in that domain still give the same f(x) values as some of those in the domain -10 ≤ x < 0, where the -x-2 portion is.
Eg.
when x = 3, f(x) = (3 - 1)² = 2² = 4
But when x = -6, f(x) = -(-6) - 2 = 6 - 2 = 4
We need to make the whole function 1-1.
Since we want the largest Df such that the inverse exists, we keep the domain [-10,0) first.
Then, find the x-coordinate for which f(x) is the same as when x = -10.
x = -10 is where the -x-2 portion has reached its maximum f(x) value of 8.
So long as the (x-1)² side has all f(x) values above 8, we will have achieved 1-to-1.
So when f(x) = 8,
(x - 1)² = 8
x - 1 = √8
(since we know the x-values are positive, we don't consider -√8)
x = 1 + √8
x = 1 + √(4x2)
x = 1 + 2√2
So for the (x-1)² portion, 1+2√2 < x ≤ 10 such that all its f(x) values are above 8. The function is now 1-to-1.
(We know that (x - 1)² is strictly increasing in the domain 1+2√2 < x ≤ 10 , from above 8 to 81)
Therefore, Df we need = [-10,0) ∪ (1+2√2,10]
(-10,0) ∪ [1+2√2,10]
In this case we are merely swapping roles
(Including x = 1 + 2√2 where f(x) = 8 and excluding x = -10 where f(x) also = 8)
For -10 ≤ x < 0, -2 < f(x) ≤ 8 instead of
8 ≤ f(x) < -2
See 1 Answer