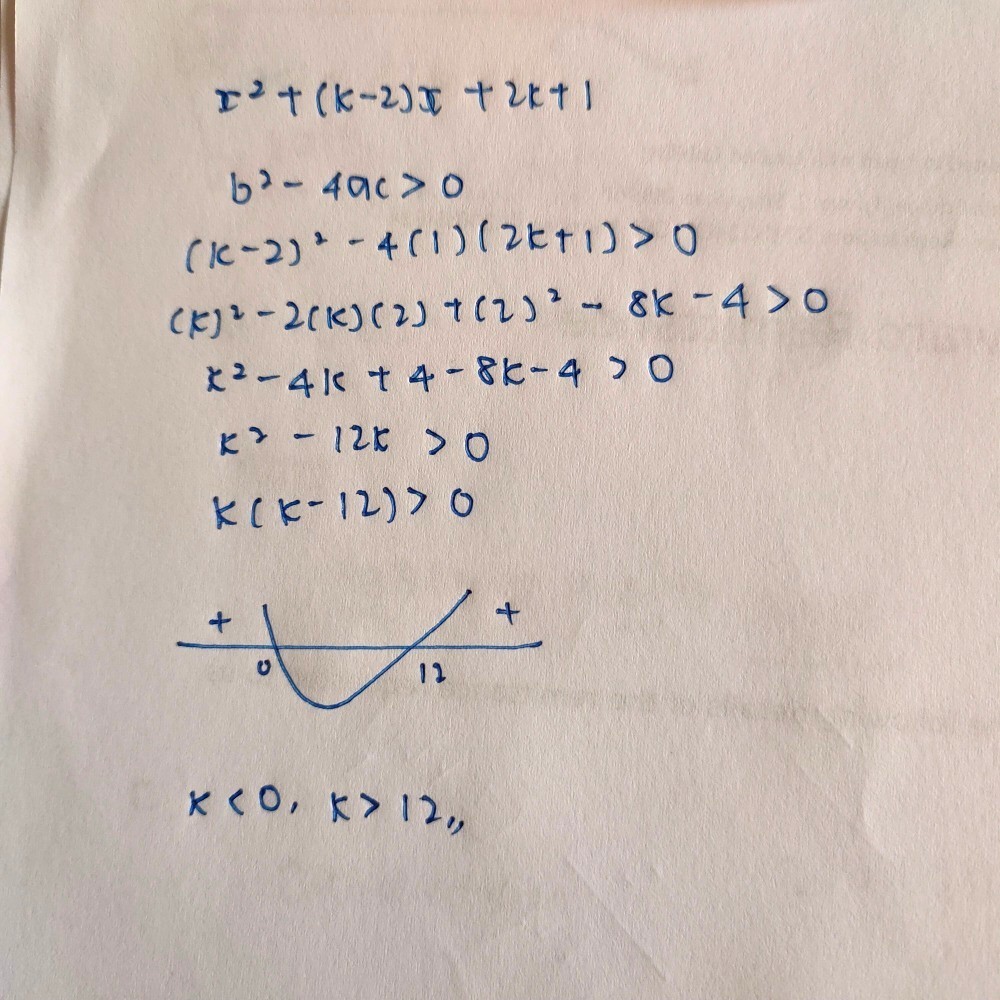Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
junior college 2 | H1 Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.
Find the sets of value for k in which x^2 + (k-2)x + 2k + 1, for all positive values of x
Need help on the above question
Date Posted: 4 years ago
Views: 687
See 1 Answer
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Answer
Date Posted:
4 years ago
Why is b^2-4ac > 0?
b2 - 4ac is, in fact, less than zero since “always positive” translates to no intersection of a graph with a horizontal axis.
QN, you should get 0 < k < 12.
QN, you should get 0 < k < 12.
So it’s 0
Yes
Thanks!!!
What's the original question? The posted photo had no words
'x² + (k-2)x + 2k + 1 is always positive'?
Please take note that 'for all positive values of x' ≠ 'always positive'. The phrasing in the caption is a bit odd.
'x² + (k-2)x + 2k + 1 is always positive'?
Please take note that 'for all positive values of x' ≠ 'always positive'. The phrasing in the caption is a bit odd.
But either way, whether it’s always positive or always negative for all real values of x, the discriminant < 0 (the coefficient of x^2 takes care of the rest).
It also can’t be the case that the expression equals zero for all real values of x.
I would, however, not think that the expression, for example, is greater than say 2 for all real values of x.
It also can’t be the case that the expression equals zero for all real values of x.
I would, however, not think that the expression, for example, is greater than say 2 for all real values of x.
For x² + (k-2)x + 2k + 1 to be always positive for all real values of x,
There is no intersection with y = 0 (also where the x-axis lies) .
There will be no real roots for x² + (k-2)x + 2k + 1 = 0
Discriminant < 0
(k-2)² - 4(1)(2k+1) < 0
k² - 4k + 4 - 8k - 4 < 0
k² - 12k < 0
k(k - 12) < 0
Either sketch the curve (upward sloping, U-shaped) intersecting the x-acis, and deduce that 0 < k < 12,
Or
Test for the sign by substituting values of k for k > 12, k< 0 and 0 < k < 12.
No need to test k = 0 and k = 12 since the product will be 0 ✖
When k > 12, eg. k = 14
Both k and k-12 are positive. Their product is also positive ✖
When k < 0, eg. k = -2
Both k and k-12 are negative. Their product is positive (>0) ✖
When 0 < k < 12 eg. k = 5
k is positive but k-12 is negative. Their product is negative (<0) ✔
So 0 < k < 12
There is no intersection with y = 0 (also where the x-axis lies) .
There will be no real roots for x² + (k-2)x + 2k + 1 = 0
Discriminant < 0
(k-2)² - 4(1)(2k+1) < 0
k² - 4k + 4 - 8k - 4 < 0
k² - 12k < 0
k(k - 12) < 0
Either sketch the curve (upward sloping, U-shaped) intersecting the x-acis, and deduce that 0 < k < 12,
Or
Test for the sign by substituting values of k for k > 12, k< 0 and 0 < k < 12.
No need to test k = 0 and k = 12 since the product will be 0 ✖
When k > 12, eg. k = 14
Both k and k-12 are positive. Their product is also positive ✖
When k < 0, eg. k = -2
Both k and k-12 are negative. Their product is positive (>0) ✖
When 0 < k < 12 eg. k = 5
k is positive but k-12 is negative. Their product is negative (<0) ✔
So 0 < k < 12
@Eric :
But what if the phrasing was :
Find the range/set of values of k where x² + (k - 2)x + 2k + 1 is always having an intersection with the x-axis?
Then b² - 4ac ≥ 0 (taking intersection to be at least at one point)
This is why knowing the original question is very important.
But what if the phrasing was :
Find the range/set of values of k where x² + (k - 2)x + 2k + 1 is always having an intersection with the x-axis?
Then b² - 4ac ≥ 0 (taking intersection to be at least at one point)
This is why knowing the original question is very important.
If the phrasing was :
'Find the set/range of values of k for which x² + (k-2)x + 2k + 1 is always positive for all positive values of x'
Only k< 0 would satisfy it.
'Find the set/range of values of k for which x² + (k-2)x + 2k + 1 is always positive for all positive values of x'
Only k< 0 would satisfy it.
For the latest example, k < 0 does not seem to always fit the situation.
For example, when k = -1, the expression becomes
x2 - 3x - 1
which is not exactly positive when x = 0 (and a tiny positive value of x)
For example, when k = -1, the expression becomes
x2 - 3x - 1
which is not exactly positive when x = 0 (and a tiny positive value of x)
Typo. It was supposed to be k > 0
The main point is, the question has to be clearly shown, if not it can't be accurately attempted in the first place.
QN wrote in the caption :
'Find the sets of value for k in which x^2 + (k-2)x + 2k + 1, for all positive values of x'
This is basically an incomplete question since the condition of the expression is not stated. Even though the range of x is given, the question is not solvable.
'Find the sets of value for k in which x^2 + (k-2)x + 2k + 1, for all positive values of x'
This is basically an incomplete question since the condition of the expression is not stated. Even though the range of x is given, the question is not solvable.
360 Tutoring Program