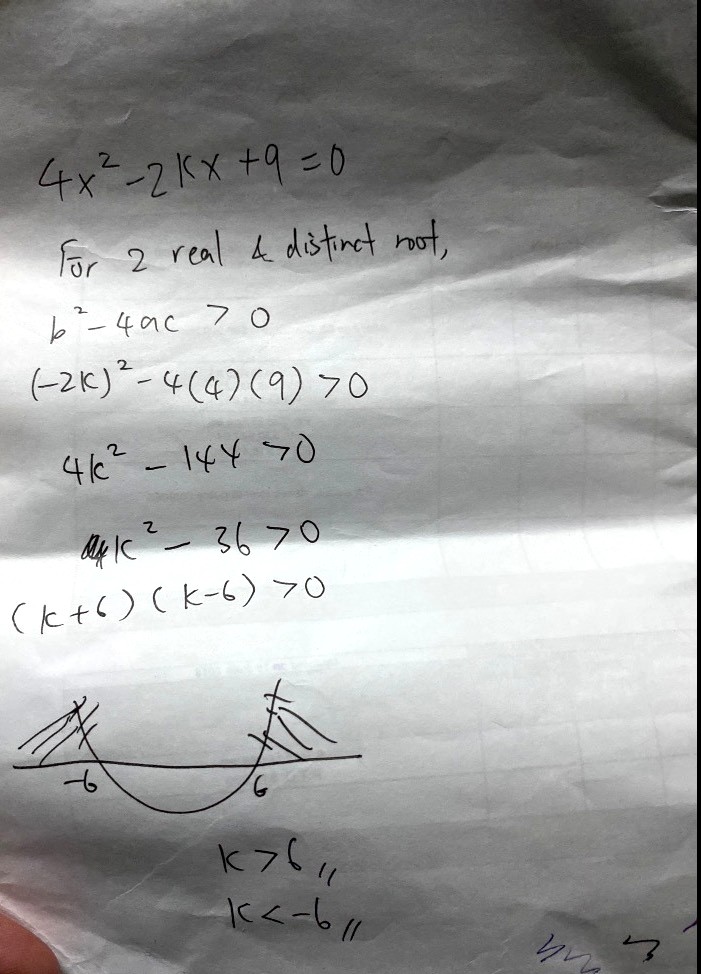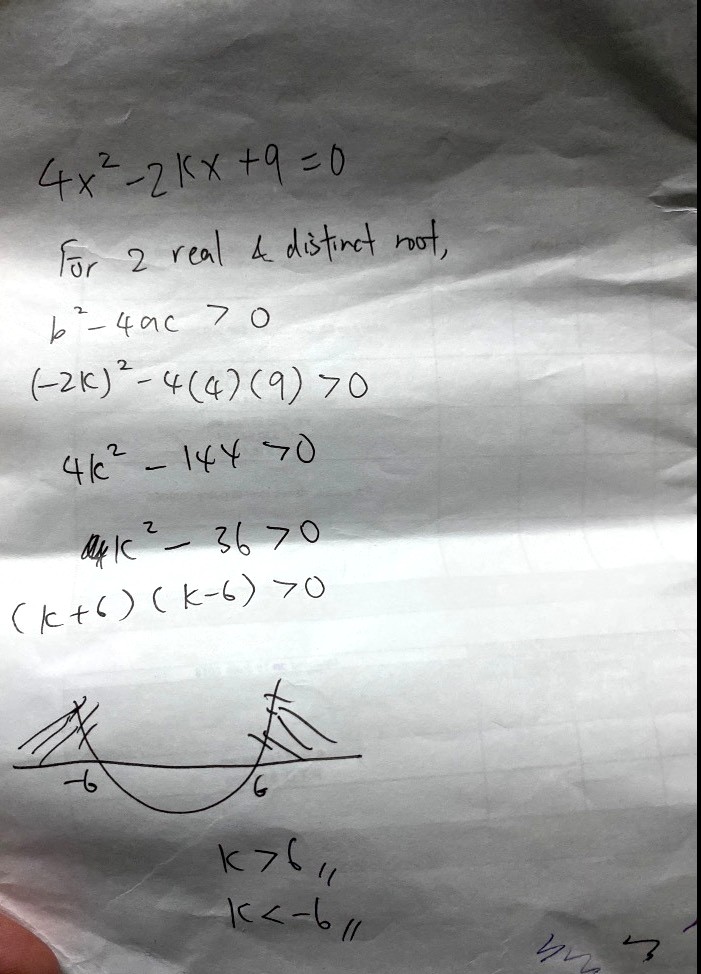4x² - 2kx + 9 = 0

For two distinct roots, discriminant > 0

For a quadratic equation ax² + bx + c = 0,

Discriminant = b² - 4ac

So (-2k)² - 4(4)(9) > 0

4k² - 144 > 0

k² - 36 > 0

(k + 6)(k - 6) > 0

k² - 36 is a upward sloping parabola
(u-shaped)

The intersection points with the y-axis are
k = 6 and k = -6.

The region between k = 6 and k = -6 is negative.

Since we want k² - 36 > 0 we want the positive region

i.e k< -6 or k > 6

What if the equation only has one real distinct root, or more than two real distinct roots?

You can't have more than 2 distinct roots for quadratic equation...

The highest power of x is 2. So the max number of roots is 2 also.

Then when does b^2 - 4ac < 0, or b^2 - 4ac = 0

For one real root only, it is what we call a repeated root.


For example ,

x² + 6x + 9 = 0
x² + 2(3)(x) + 3² = 0

(x + 3)² = 0

(x + 3)(x + 3) = 0

x = 3 or x = 3

For such cases, b² - 4ac = 0

b² - 4ac < 0 is when there are no real roots

(i.e the roots are in the form of complex numbers, where terms like i are used.

i = √-1, which is non-real. stands for imaginary)

Likewise, i² = -1

So is it true to say that when b^2 - 4ac < 0, there exists no solution to the question

Seems like you're not familiar with A Math syllabus.

For a quadratic equation ax² + bx + c = 0,

x² + (b/a) x + c/a = 0

x² + 2(b/2a) x + (b/2a)² + c/a = (b/2a)²

(x + b/2a)² + c/a = (b/2a)²

(x + b/2a)² = b²/4a² - c/a

(x + b/2a)² = (b² - 4ac)/4a²

x + b/2a = ±√((b² - 4ac)/4a²)

x + b/2a = ± √(b² - 4ac) / 2a

x = -b/2a ± √(b² - 4ac) / 2a

x = (-b ± √(b² - 4ac) ) / 2a


This is the famous quadratic formula.

x = (-b ± √(b² - 4ac)) / 2a


① When b² - 4ac > 0, the term inside the square root is positive.

So we can get a real number. and the ± means there are 2 unique real solutions /real roots to the equation.


② When b² - 4ac = 0, square root of 0 is still 0.

So x = (-b±0) / 2a = -b/2a

There is only one real solution/root.


③ When b² - 4ac < 0, the inside of the square root is negative.

There are no real solutions/real roots to the equation. The solutions are what we called complex numbers (a combo of real and imaginary numbers)

Here's an example of a 'no real roots' equation :

x² + 2x + 3 = 0

Here a = 1, b = 2 , c = 3

Using quadratic formula,

x = [ -2 ± √(2² - 4(1)(3) ) ] / 2(1)

x = [-2 ± √-8] / 2

x = -1 ± √-8 / 2

x = -1 ± √((4)(2)(-1)) / 2

x = -1 ± √4√2√-1 / 2

x = -1 ± 2√2√-1 / 2

x = -1 ± √2√-1

Typically at O level we will stop here and say that there are no real roots to the equation, since a square root of a negative number means it is non-real.

Yes, and to prove that there is no real roots, I have to prove b^2 - 4ac < 0?

The other way is to complete the square.


x² + 2x + 3 = 0

x² + 2x + 1 + 2 = 0

(x + 1)² + 2 = 0

(x + 1)² = -2

x + 1 = ± √-2

x = -1 ± √-2


At O level we will stop here and say there are no real roots/solutions to the equation.


BUT, at H2 Math in A levels (perhaps not applicable to H1) ,

x = -1 ± √-2

x = -1 ± √((2)(-1))

x = -1 ± √2 √-1

x = -1 ± √2 i

Yes, if you show that b² - 4ac < 0, it means discriminant < 0

(b² - 4ac is the formula. Discriminant is the name)

Then you can say that there are no real roots/solutions to the equation.