Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 2 | H1 Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Need help
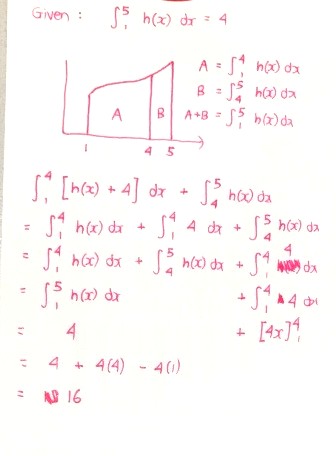
5 1 h(x) dx
Correct is
integrate (from 1 to 4)
OPEN BRACKET h(x) + 4 CLOSE BRACKET
dx
Without the open bracket and the close bracket to cover the h(x) + 4, the presentation is wrong.
The question is poorly presented by the setter.
In the A Levels it would be placed as well. Otherwise, if the question is viewed by an external party, the external party may feel that A Level is capable of publishing errors in a paper
When you take higher level mathematics modules (H3 or university modules) or even encounter graduate level texts or research paper, you'll see the brackets not being there very often.
It is considered optional as it is understood that the integral is taken over the whole expression (it is already between the integral symbol and the dx anyway)
∫ x² cos 3x dx
In this case it is understood to mean
∫ (x² cos (3x) ) dx
∫(UL: b, LL: a) f(x) dx + ∫(UL: c, LL: b) f(x) dx
= ∫(UL: c, LL: c) f(x) dx
Can the same be said for
∫(UL: b, LL: a) f(x) dx - ∫(UL: c, LL: b) f(x) dx
= F(b) - F(a) + F(c) - F(b)
= F(c) - F(a)
= ∫ (lower a , upper c) f(x) dx
(F(a) means the value of of the integral of f(x) when x = a)
∫(lower a, upper c) f(x) dx - ∫(lower b, upper c) f(x) dx
= ∫(lower a, upper b) f(x) dx
We could also do this :
∫(lower a, upper c) f(x) dx - ∫(lower b, upper c) f(x) dx
= ∫(lower a, upper c) f(x) dx - (- ∫(lower c, upper b) f(x) dx
= ∫(lower a, upper c) f(x) dx + ∫(lower c, upper b) f(x) dx
= ∫(lower a, upper b) f(x) dx
http://output.to/sideway/default.aspx?qno=111000019
In this website you'll see the proofs for the various properties
∫ (lower a, upper b) f(x) dx - ∫(lower b, upper c) f(x) dx
= F(b) - F(a) - ( F(c) - F(b) )
= F(b) - F(a) - F(c) + F(b)
= 2F(b) - F(a) - F(c)
So the same cannot be said for subtraction as with addition
See 1 Answer