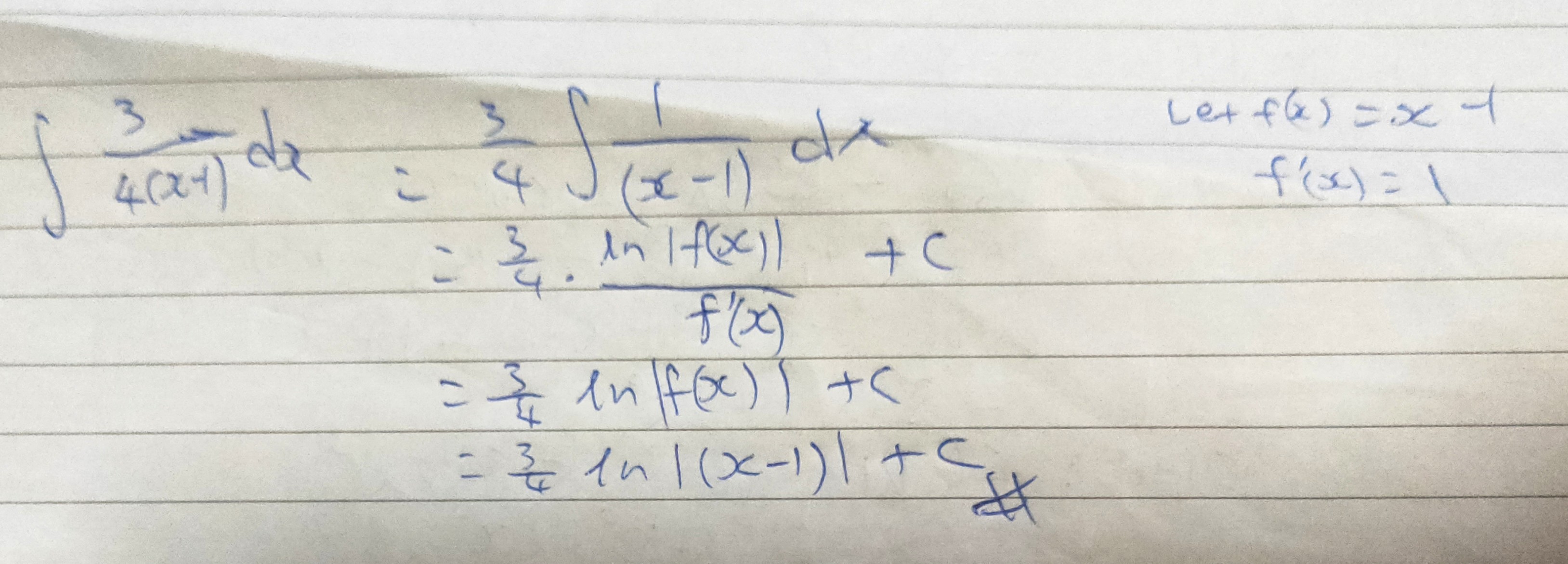Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
junior college 2 | H1 Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.
Need help
Date Posted: 4 years ago
Views: 397
See 1 Answer
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
3/(4(x-1)) is also equals to (0.75)((x-1)^-1). So, apply integral of 1/f(x) which is ln(f(x))/f'(x) +c. Hope it helps!
Date Posted:
4 years ago
Anyway why divide first derivative of f(x) is due to reverse chain rule.
Can I expand 4(x-1) first then integrate 3/(4x-4)?
∫3/4(x-1) dx
= 3 ∫(4x-4)^-1
= 3.1/4 ln|4x-4|+ c
= 3/4 ln|4x-4|+ c
∫3/4(x-1) dx
= 3 ∫(4x-4)^-1
= 3.1/4 ln|4x-4|+ c
= 3/4 ln|4x-4|+ c
Integration of 1/f(x) dx in a more general term is ∫f'(x)/f(x)dx =ln lf(x)l +c . So ∫3/4(x-1) dx = 3/4 ∫4/(4x-4)dx to fit into the form of ∫f'(x)/f(x)dx is also equals to 3/4 ∫1/(x-1)dx to fit into ∫f'(x)/f(x)dx. So 3/(4x-4) is not correct as by expanding, you are changing the power base. You have to ensure in ax+b, it cannot be simplified further as I understand your question as if it is asking for 3/4*1/x-1.
∫1/(ax+b) dx =1/a(ln(ax+b)) + c
Therefore if you expand, it is 3/(ax+a) dx where a=4. It doesn't fit into the rule anymore. 3/a* (Ax+b) fits into ∫1/(ax+b) dx. Where A is the coefficient of x which is 1 in this case, and b is -1.
Therefore if you expand, it is 3/(ax+a) dx where a=4. It doesn't fit into the rule anymore. 3/a* (Ax+b) fits into ∫1/(ax+b) dx. Where A is the coefficient of x which is 1 in this case, and b is -1.
No wonder. Thanks for the explanation!
360 Tutoring Program