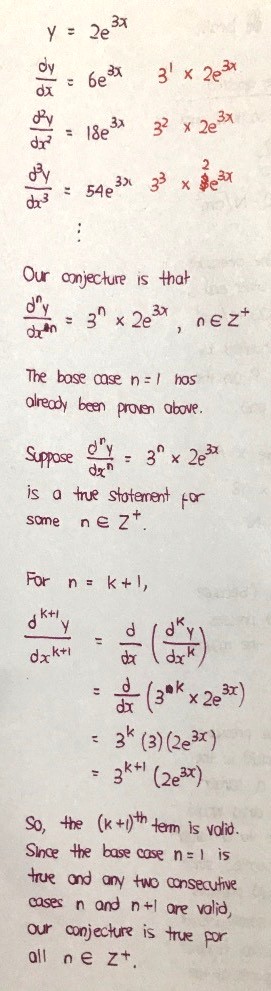Later once my class finishes I write for you the steps to look out for when you attempt to do proof by induction.

Ok, the idea goes like this when we do mathematical induction and we have an equation to prove.

1. We need to prove that the base case (often n = 1) is true.

2. We are going to assume that the kth statement is true for some value of k (sorry, I wrote wrongly on my paper)

3. We are going to prove that the (k + 1)th case is true by doing a series of simplifications. We cannot just write the (k + 1)th statement immediately and say that it’s proven. Rather, we need to work out way out.

4. The third step above establishes that any two pairs of consecutive cases k and k + 1 will hold for any choice of k. Combined with the first step, this means that

- since the first statement (k = 1) is true, the second statement (k + 1 = 1 + 1 = 2) is true

- since the second statement (k = 2) is true, the third statement (k + 1 = 2 + 1 = 3) is true

- since the third statement (k = 3) is true, the fourth statement (k + 1 = 3 + 1 = 4) is true.

- and so on, infinitely.

So, this means that every single choice of k works.

As such, our equation has been proven by the method of induction.