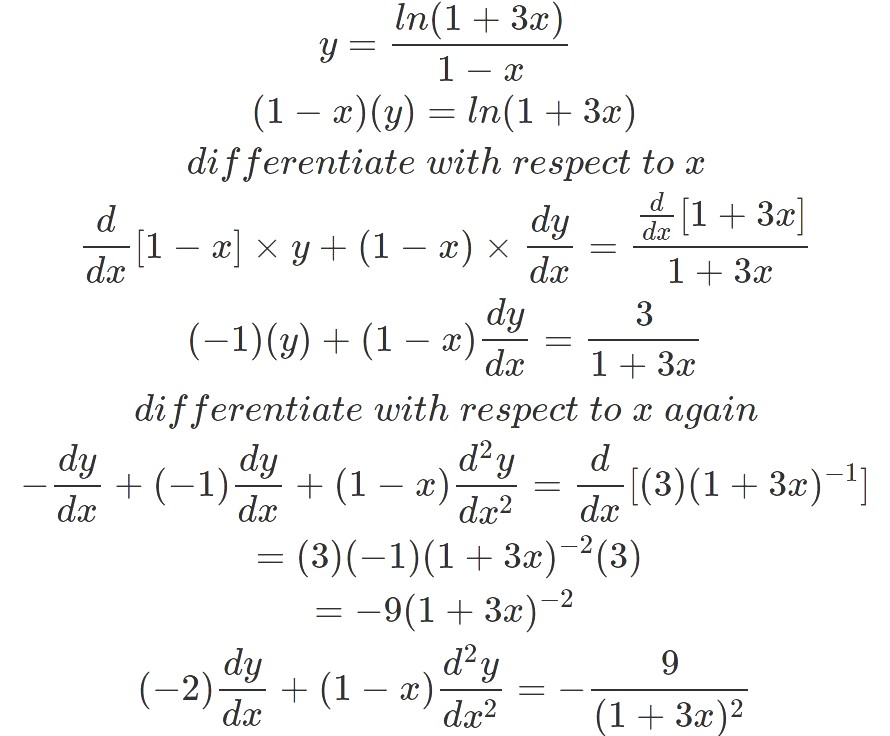y = ln(1 + 3x)/(1 - x)

(1 - x)y = ln(1 + 3x)

Differentiate with respect to x,

(1 - x)dy/dx + (-1)y = 3/(1 + 3x)

(1 - x)dy/dx - y = 3/(1 + 3x)

Differentiate with respect to x,

(1 - x)d²y/dx² + (-1)dy/dx - (1)dy/dx = -3(3)/(1 + 3x)²

(1 - x)d²y/dx² - 2dy/dx = -9/(1 + 3x)²

(1 - x)d²y/dx² + 9/(1 + 3x)² = 2dy/dx

(Shown)

From part one we know the following :

y = ln(1 + 3x)/(1 - x) ①

(1 - x)dy/dx - y = 3/(1 + 3x) ②

(1 - x)d²y/dx² + 9/(1 + 3x)² = 2dy/dx ③


We also know the Maclaurin expansion :

f(x) = f(0) + xf'(0) + x²/2! f''(0) + x³/3! f'''(0) + ...

Letting y = f(x),
dy/dx = f'(x), d²y/dx² = f''(x), d³y/dx³ = f'''(x)


Sub x = 0 into ①,
y = ln(1 + 3(0))/(1 - 0)
= ln 1
= 0

This is f(0)


Sub x = 0, y = 0, into ②,
(1 - 0)dy/dx - 0 = 3/(1 + 3(0))
dy/dx = 3/1 = 3

This is f'(0)


Sub x = 0, y = 0, dy/dx = 3 into ③,

(1 - 0)d²y/dx² + 9/(1 + 3(0))² = 2(3)
d²y/dx² + 9 = 6
d²y/dx² = -3

This is f''(0)

From ③,(1 - x)d²y/dx² + 9/(1 + 3x)² = 2dy/dx

Differentiate with respect to x,

(1 - x)d³y/dx³ + (-1)d²y/dx² + 9(-2)(3)/(1 + 3x)³ = 2d²y/dx²

(1 - x)d³y/dx³ - d²y/dx² - 54/(1 + 3x)³ = 2d²y/dx²

(1 - x)d³y/dx³ - 54/(1 + 3x)³ = 3d²y/dx²


Sub x = 0, y = 0, dy/dx = 3, d²y/dx² = -3,

(1 - 0)d³y/dx³ - 54/(1 + 3(0))³ = 3(-3)

d³y/dx³ - 54 = -9
d³y/dx³ = 45

This is f'''(0)



So,

y = f(x) = f(0) + xf'(0) + x²/2! f''(0) + x³/3! f'''(0) + ...

y = 0 + x(3) + x²/2! (-3) + x³/3! (45) + ...

y = 3x - 3/2 x² + 15/2 x³ + ...

Edited

Standard series

For ln (1 + x) : x - x²/2 + x³/3 +...

For (1 + x)ⁿ : 1 + nx + n(n - 1)/2! x² + n(n - 1)(n - 2)/3! x³ + ...


So,

y = ln(1 + 3x)/(1 - x)

y = ln(1 + 3x) (1 - x)-¹

= [3x - (3x)²/2 + (3x)³/3 + ...] [1 + (-1)(-x) + (-1)(-2)/2! (-x)² + (-1)(-2)(-3)/3! (-x)³ +...]

= [3x - 9/2 x² + 9x³ + ...] [1 + x + x² + x³ +...]

= 3x(1) + 3x(x) + 3x(x²) - 9/2 x² (1) - 9/2 x² (x) + 9x³(1) + ...

= 3x + 3x² + 3x³ - 9/2 x² - 9/2 x³ + 9x³

= 3x - 3/2 x² + 15/2 x³ + ...

(verified)

Set of values for which (1 - x)-¹ is valid :

|-x| < 1

|x| < 1

-1 < x < 1


Set of values for which ln(1 + 3x) is valid :

-1 < 3x ≤ 1

-⅓ < x ≤ ⅓

Combining the two ,


-⅓ < x ≤ ⅓