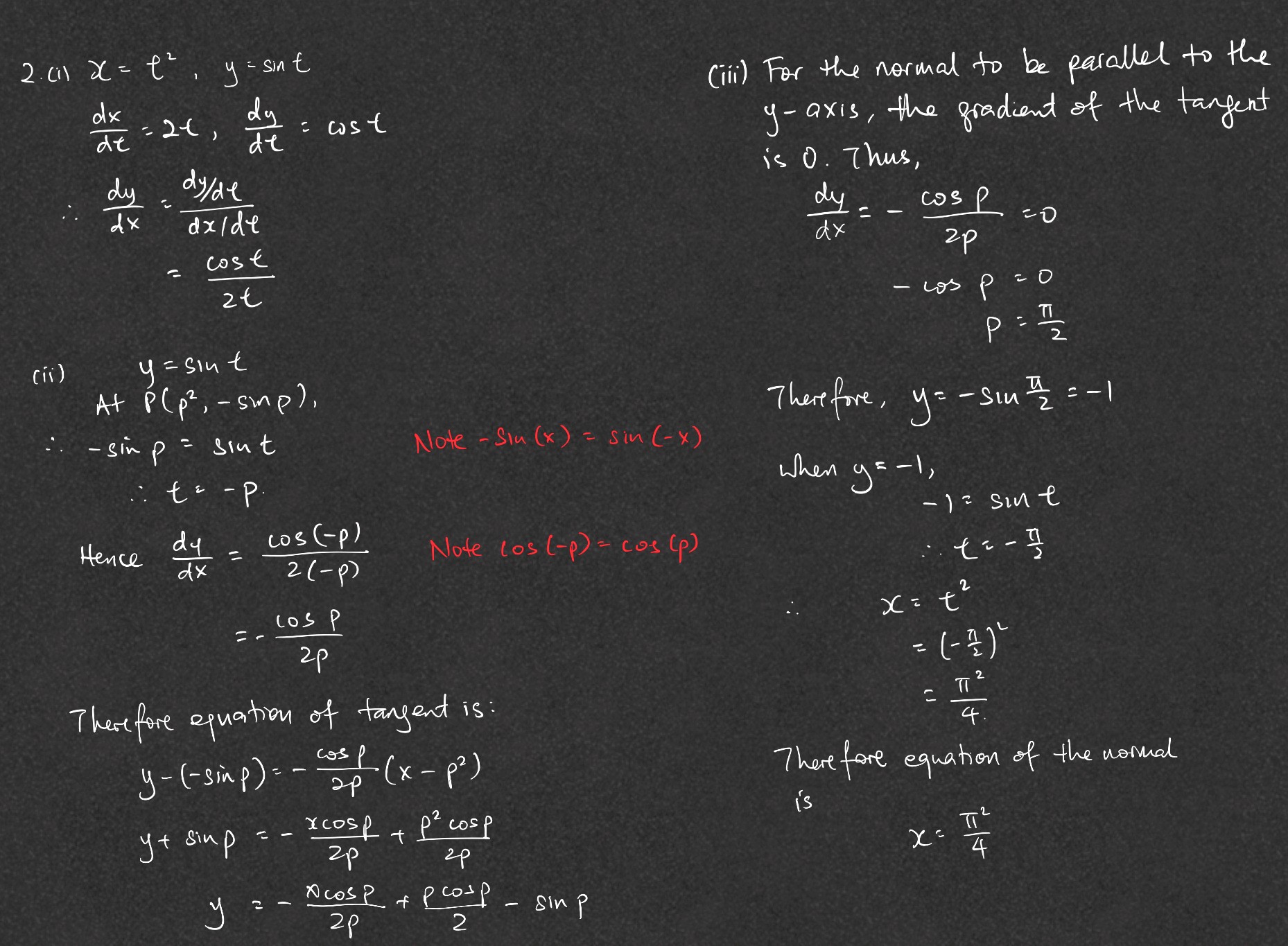y - x + 3e^(-y) = 3

Differentiate both sides with respect to x,


dy/dx - 1 - 3e^(-y) (dy/dx) = 0

dy/dx - 3e^(-y) (dy/dx) = 1

dy/dx (1 - 3e^(-y)) = 1

dy/dx = 1/(1 - 3e^(-y))


At (0,0), y = 0
Sub y = 0,

dy/dx = 1/(1 - 3e^0)

= 1/(1 - 3)

= -½

This is the gradient of the tangent to the point (0,0)

Gradient of the normal = -1/(-½)
= 2

Since the normal passes through the point (0,0), the y-intercept is 0.

Equation of a straight line is y = mx + c

The normal to the curve is a straight line. In this case the gradient of the normal is 2 and the y-intercept is 0. So m = 2 and c = 0

Equation of normal is therefore

y = 2x

Implicit differentiation is the same as normal differentiation. It's just applying the chain rule.


For example, let's say y = x²,
and dy/dx = 2x

Then y³ = (x²)³ = x^6

If you were to differentiate y³ with respect to y, you would get 2y².

if you were to differentiate x^6 directly with respect to x, you would get 6x^5 directly.

But if you were to differentiate the form (x²)³, you'll use the chain rule instead, and

d/dx (x²)³
= 3(x²)²(2x)
= 3x⁴(2x)
= 6x^5 ①


Now, if you were to differentiate y³ with respect to x instead,

You'll have to differentiate y³ as well as the the term y as per the chain rule, since y is a function of x.

so d/dx (y³)

= 3y² dy/dx

= 3(x²)² (2x)

= 3x⁴ (2x)

= 6x^5

Notice we are doing the same steps as in ①