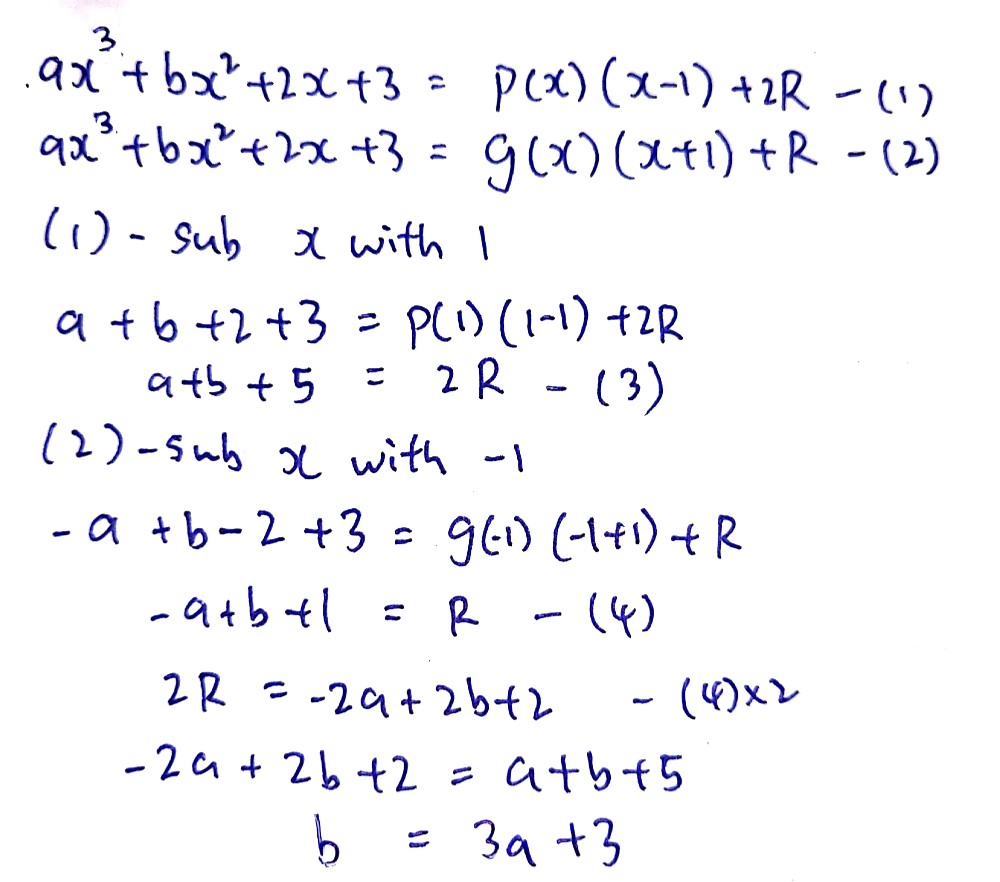Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
secondary 3 | A Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.
This is under polynomials help pls
Date Posted: 4 years ago
Views: 289
See 2 Answers
This chapter has 2 fundamental theories that would make such questions very manageable.
1) factor theorem: for any f(x), if (x-a) [where a is element of real number] is a factor, f(a)=0 where 0 denotes 0 remainder.
— use this when you need to prove for factors
2) remainder theorem: for any f(x), if (x-a) [where a is element of real number] is NOT a factor, f(a)=remainder.
— use this when you need to find remainders when polynomial is divided by a certain (x-a)
**f(a) means you sub in value “a” into all “x”.
** if required to divide polynomial by x^2,x^3... etc cannot use f(a) anymore have to use long division.
*** the previous answer is another way of representing the polynomial and is worth studying and understanding what it means because some questions require that knowledge of forming polynomials as F(x)=quotient•dividend+remainder.
1) factor theorem: for any f(x), if (x-a) [where a is element of real number] is a factor, f(a)=0 where 0 denotes 0 remainder.
— use this when you need to prove for factors
2) remainder theorem: for any f(x), if (x-a) [where a is element of real number] is NOT a factor, f(a)=remainder.
— use this when you need to find remainders when polynomial is divided by a certain (x-a)
**f(a) means you sub in value “a” into all “x”.
** if required to divide polynomial by x^2,x^3... etc cannot use f(a) anymore have to use long division.
*** the previous answer is another way of representing the polynomial and is worth studying and understanding what it means because some questions require that knowledge of forming polynomials as F(x)=quotient•dividend+remainder.
360 Tutoring Program