Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

See 1 Answer
done
2 Upvotes
clear 0 Downvotes
I have done completing the square all the way.
For the last part, we see that f’(x), which equals to -2 [cos x/2 - 1]^2 - 1, has a greatest value of -1. This is because the lowest value of the squared expression is 0, and multiplying the squared expression by a negative number makes the greatest value zero.
So, f’(x) <= -1 < 0 for all x > 0.
And, when x = 0, f(x) = 8 sin 0 - sin 0 - 0 = 0.
Since f(x) = 0 and the gradient function f’(x) is always negative for all x > 0, f(x) < 0 for all real x > 0.
For the last part, we see that f’(x), which equals to -2 [cos x/2 - 1]^2 - 1, has a greatest value of -1. This is because the lowest value of the squared expression is 0, and multiplying the squared expression by a negative number makes the greatest value zero.
So, f’(x) <= -1 < 0 for all x > 0.
And, when x = 0, f(x) = 8 sin 0 - sin 0 - 0 = 0.
Since f(x) = 0 and the gradient function f’(x) is always negative for all x > 0, f(x) < 0 for all real x > 0.
Date Posted:
4 years ago




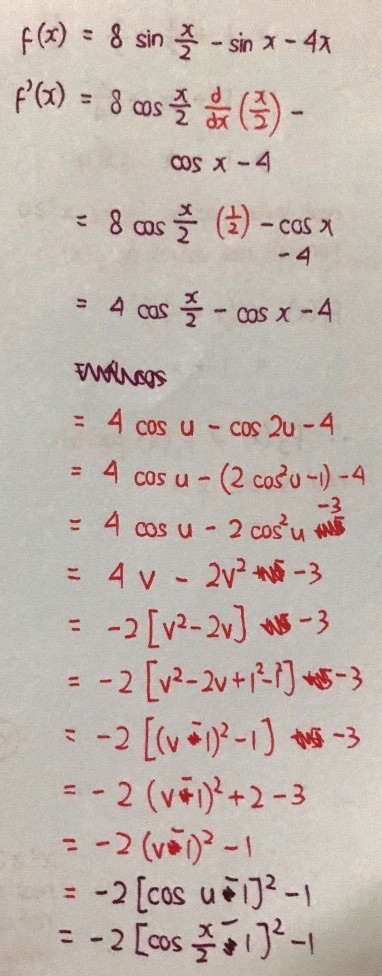

This is why we must also check the point when x = 0 to make sure it is not on the positive side.